10年積累的網(wǎng)站設(shè)計制作、網(wǎng)站制作經(jīng)驗，可以快速應(yīng)對客戶對網(wǎng)站的新想法和需求。提供各種問題對應(yīng)的解決方案。讓選擇我們的客戶得到更好、更有力的網(wǎng)絡(luò)服務(wù)。我雖然不認識你，你也不認識我。但先網(wǎng)站設(shè)計制作后付款的網(wǎng)站建設(shè)流程，更有臨洮免費網(wǎng)站建設(shè)讓你可以放心的選擇與我們合作。寫在前面

藍橋杯省賽將在4月初舉行，距離比賽也就剩一個多月的時間。為了提高自己的編程能力，在比賽中取得比較👌的成績。接下來的一個多月我會在博客中更新藍橋杯的學(xué)習(xí)。爭取在考前將一些重要的算法過一遍。

藍橋杯常考的算法我整理到了一張思維導(dǎo)圖里面，小伙伴可以看一下噢。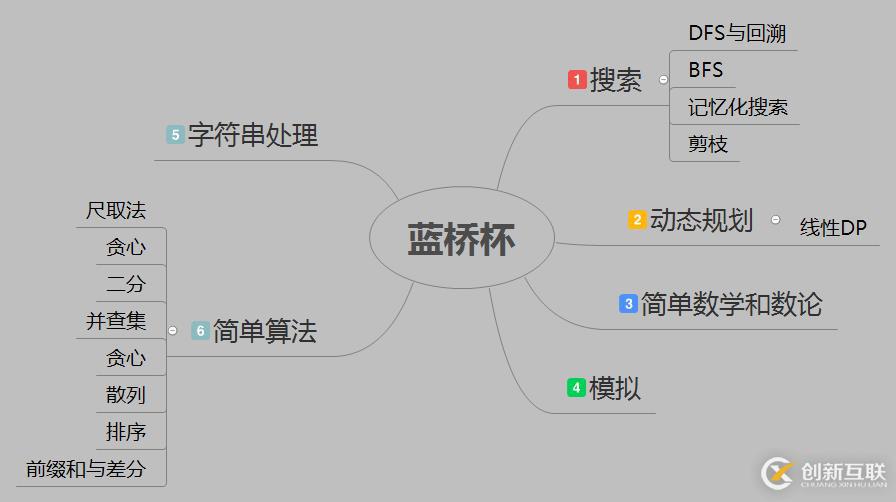

這張藍橋杯思維導(dǎo)圖可能不太全面，以后會經(jīng)常補充的。。

我是這樣想滴，我會對常考的算法做個專題總結(jié)，分專題來講。文章更新的速度呢取決于我刷題的速度啦！ 因為每寫一個專題必然要寫運用到這種算法的題目啦~魯迅先生說過“只講解算法思想，不實際運用就是在耍流氓”。寫藍橋杯文章的過程是這個樣子的，先確定要寫哪個專題，然后呢大量刷題，模板題啦，經(jīng)典題啦，最最重要的是歷屆的藍橋杯真題啦。刷完之后呢做總結(jié)理清這種算法的基本思路，最后就形成了一篇藍橋杯備考文章啦。當(dāng)然文章是要時常更改補充的，因為在刷題的過程中可能對某些算法思想有了新的感悟~也要參加藍橋杯的小伙伴們可以一起期待噢，關(guān)注我一定不會讓你失望的。噢還有我參加的是C++組所以呢我寫的題解也是C++的。

我的博客 https://blog.csdn.net/ccevv/

---

好啦接下來進入正題。

我們知道藍橋杯俗稱暴力杯，搜索在藍橋杯中是最最基本的算法思想。學(xué)會DFS和BFS是在藍橋杯比賽中取得好成績的基礎(chǔ)。我會從這幾個方面入手，給小伙伴們詳細講解搜索專題。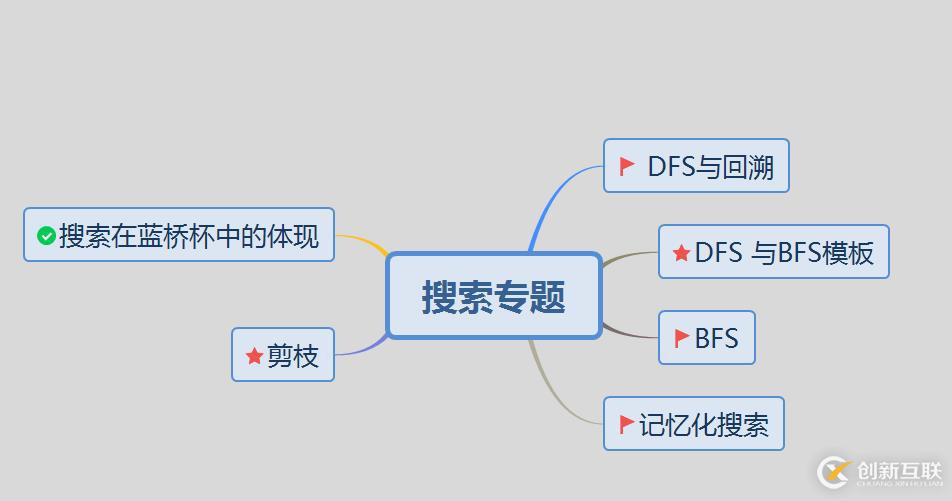

本篇的內(nèi)容主要有以下幾個方面噢，小伙伴們可以有個大致了解。

DFS基本思想(DFS+回溯）
深度優(yōu)先搜索模板
DFS例題
剪枝思想
剪枝思想在DFS中的應(yīng)用

---

文章目錄

• 寫在前面
• • 一、深度優(yōu)先搜索(DFS)+回溯
  • 二、DFS模板
  • 三、DFS經(jīng)典例題
  • • 1.模板題——迷宮問題
    • 2.01背包問題(DFS暴力搜索)
    • 3.回溯——[USACO1.5]八皇后 Checker Challenge
    • 4.遞歸實現(xiàn)排列型枚舉
    • 5.遞歸實現(xiàn)組合型枚舉
  • 四、剪枝思想
  • 五、剪枝思想在DFS中的應(yīng)用
• 寫在后面

---

一、深度優(yōu)先搜索(DFS)+回溯

DFS是一種搜索的策略，簡單來說就是一條路走到黑。當(dāng)走到盡頭之后就回退到上一個結(jié)點，繼續(xù)一條路走到黑。回退的過程就叫做回溯。
DFS一般采用遞歸的方式實現(xiàn)。

對遞歸的詳細講解會在以后出一個獨立的專題，小伙伴們可以期待一下噢！

DFS可以用一個遞歸搜索樹來形象描述，那這棵樹長什么樣子呢，小伙伴們繼續(xù)往下看。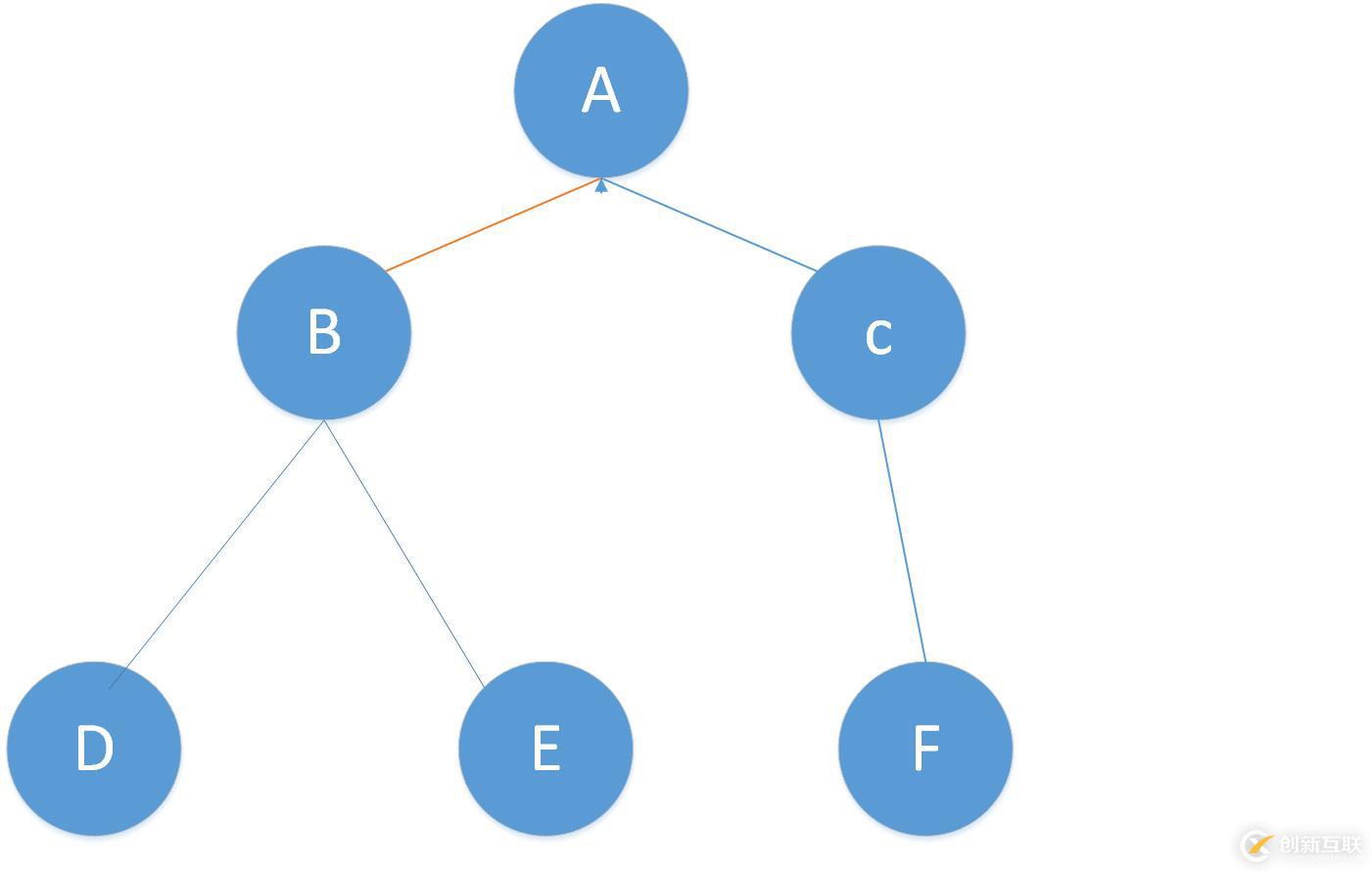

事實上對所有的合法DFS求解過程都可以把它畫成樹的形式，死胡同就相當(dāng)于葉子結(jié)點。分岔口就相當(dāng)于非葉子結(jié)點。

對某個DFS類型的題目，不妨把一些狀態(tài)作為樹的結(jié)點，問題就變得很直觀了。

DFS搜索的順序是A-B-D-E-C-F。從結(jié)點A出發(fā)，它有兩條路可以走，我們選擇最左邊那一條，到達結(jié)點B，結(jié)點B有兩個分支，選擇最左邊那個，到達結(jié)點D。結(jié)點D沒有路可走了也就是到達死胡同了，返回上一個結(jié)點B，也就是回溯的過程。B還有一條路可走，到達結(jié)點E。同理結(jié)點E回溯到結(jié)點B，結(jié)點B沒有分支了，回溯到上一個結(jié)點A，結(jié)點A還有一個分支可以走，到達結(jié)點C,結(jié)點C有一個分支到達結(jié)點F，結(jié)點F是死胡同。至此所有的結(jié)點都訪問了，搜索結(jié)束。

其實DFS的搜索順序和樹的先序遍歷是一樣的。樹的先序遍歷就是根左右。

從遞歸樹我們就能看出DFS的時間復(fù)雜度是很高的，是 O ( 2 n ) O(2^n) O(2n)。所以我們常說暴力搜索嘛，就是因為它時間復(fù)雜度太高了，當(dāng)數(shù)據(jù)很大時很容易就TLE(超時)的。同時我們還能看出DFS會走遍所有的路徑，并且走到死胡同就代表一條完整的路徑形成。因此深度優(yōu)先搜索是一種枚舉所有路徑，遍歷所有情況的搜索策略。

---

二、DFS模板

在備戰(zhàn)藍橋杯的過程中記住一些算法模板還是非常重要滴。

#includeusing namespace std;
bool check()
{...
}
void dfs()
{if (滿足邊界條件)
	{		return;
	}
	for (int i = 0; i< 可擴展的路徑數(shù); i++)
	{if (check())
		{	修改現(xiàn)場;
			dfs(下一種情況);
			還原現(xiàn)場;
		}
	}
}	

模板不是固定不變的，我們要根據(jù)題目靈活地運用它。

---

三、DFS經(jīng)典例題 1.模板題——迷宮問題

題目鏈接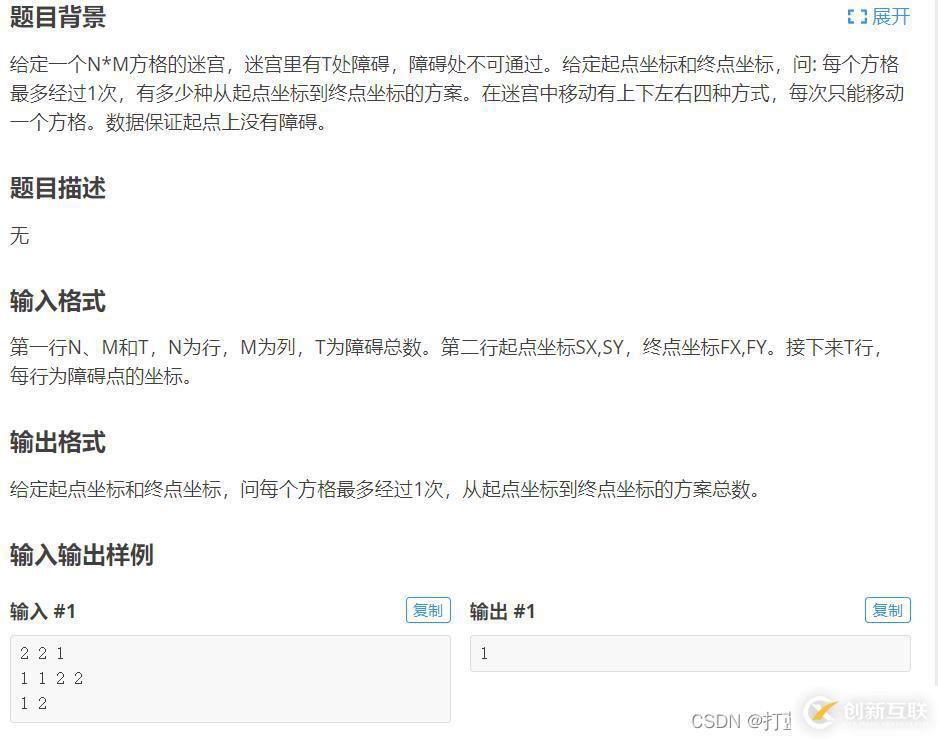

題目分析

迷宮問題是拿來練習(xí)DFS與BFS很經(jīng)典的題目。迷宮問題有很多種問法，比如迷宮從起點到終點有沒有路徑，有幾條，最短路徑是多少。

求從起點到終點的方案數(shù)顯而易見也是要用DFS，遍歷所有的情況。我們要考慮這樣一個問題，迷宮里的某點(x,y)是否要被訪問呢。當(dāng)這點是障礙物肯定不能訪問，該點不在迷宮里面也不能訪問，該點訪問過了那就不能訪問了。(題目中有每個方格最多經(jīng)過一次)。因此我們需要一個check()函數(shù)來判斷某一點是否合法。合法我們就去訪問該點。

其實這個過程就是一個剪枝的過程，根據(jù)題目條件限制，剪掉一些不可能存在解的分支。

另外我們該如何知道某點是障礙點呢，可以設(shè)置一個map數(shù)組來表示該迷宮。

• 當(dāng)map[x][y]==1時表示該點是障礙點
• map[x][y]==0表示該點是正常點

AC代碼

#includeusing namespace std;

const int N = 100;

int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};//方向數(shù)組技巧
int n, m, T;//n行m列T障礙總數(shù)
int ans;//記錄方案總數(shù)
int sx, sy, fx, fy, l, r;//起點坐標(sx,sy)終點坐標(fx,fy)障礙點坐標(l,r)
bool visited[N][N];//記錄某點是否被訪問過
int map[N][N];//map[i][j] == 1表示是障礙

bool check(int x, int y)//check某點是否合法
{if (x< 1 || x >n || y< 1 || y >m) return false;//該點出界不合法
    if (map[x][y]) return false;//該點是障礙點不合法
    if (visited[x][y]) return false;//該點被訪問過不合法
    return true;//其他情況訪問合法
}

void dfs(int x, int y)//dfs維護點的坐標參數(shù)
{if (x == fx && y == fy)//滿足邊界條件，到達終點
    {ans++;//方案數(shù)+1
        return;
    }
    for (int i = 0; i< 4; i++)//枚舉四個方向
    {int newx = x + dx[i];
        int newy = y + dy[i];
        if (check(newx, newy))//該點合法
        {visited[x][y] = true;//將(x,y)設(shè)置成已訪問,修改現(xiàn)場
            dfs(newx, newy);//dfs下一個點
            visited[x][y] = false;//回溯,恢復(fù)現(xiàn)場
        }
    }
}

int main()
{cin >>n >>m >>T;
    cin >>sx >>sy >>fx >>fy;
    while(T--)
    {cin >>l >>r;
        map[l][r] = 1;
    }
    dfs(sx, sy);//從起點開始搜索
    cout<< ans<< endl;
    return 0;
}

小伙伴們每道例題都要好好看一下AC代碼噢，上面有很詳細的注釋。

這道題還可以優(yōu)化下空間，可以只用maze數(shù)組來表示迷宮，同時記錄迷宮內(nèi)的某點是否訪問過。具體見下面的代碼。

//空間優(yōu)化
#includeusing namespace std;

const int N = 100;

int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};//方向數(shù)組
int n, m, T;
int ans;
int sx, sy, fx, fy, l, r;
//bool visited[N][N];
int map[N][N];//map[i][j] == 1表示是障礙
                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                          
bool check(int x, int y)//判斷某點是否可以訪問
{if (x< 1 || x >n || y< 1 || y >n) return false;
    if (map[x][y] || map[x][y] == 3 ) return false;//該點是障礙點或已經(jīng)訪問過，不能訪問
    //if (visited[x][y]) return false;
    return true;
}

void dfs(int x, int y)
{if (x == fx && y == fy)
    {ans++;
        return;
    }
    for (int i = 0; i< 4; i++)
    {int newx = x + dx[i];
        int newy = y + dy[i];
        if (check(newx, newy))
        {map[x][y] = 3;//標記成已訪問
            dfs(newx, newy);
            //點(x,y)能訪問說明它不是障礙點所以回溯要讓map[x][y]=0
            //而不是map[x][y]=1
            map[x][y] = 0;
        }
    }
}
int main()
{cin >>n >>m >>T;
    cin >>sx >>sy >>fx >>fy;
    while(T--)
    {cin >>l >>r;
        map[l][r] = 1;
    }
    dfs(sx, sy);
    cout<< ans<< endl;
    return 0;
}

2.01背包問題(DFS暴力搜索)

題目鏈接

題目分析

01背包問題是一個很經(jīng)典的問題，它有多種解法。DFS是其中一種，在學(xué)習(xí)動態(tài)規(guī)劃的時候還會提到它噢。

第i件物品無非就是選和不選兩種情況，在搜索的過程中DFS函數(shù)必須要記錄當(dāng)前處理的物品編號index，當(dāng)前背包的容量sumW，當(dāng)前的總價值sumC。

• 當(dāng)不選第index個物品時，那么sumW,sumC是不變的，接著處理第index+1個物品，也就是DFS(index+1, sumW, sumC)。
• 當(dāng)選擇第index個物品時，sumW變成sumW+w[index]，sumC變成sumC+v[index]，接著處理第index+1個物品，也就是DFS(index+1, sumW+w[index],sumC+v[index])。邊界條件也就是把最后一件物品也處理完了，即index=n（注意默認index從0開始）。

當(dāng)一條分支結(jié)束了該干什么呢，很簡單呀就是判斷該分支最終滿不滿足總重量不大于背包容量。即sumW<=v。滿足的話我們就更新價值maxvalue，即maxvalue=max(maxvalue,sumC)。

AC代碼

//01背包問題的dfs版本
#include#include 

using namespace std;

const int N = 10010;
int n, v, maxvalue;
int w[N], c[N];
//DFS維護三個參數(shù)，正在選第index個物品，當(dāng)前的總體積，當(dāng)前的總價值
void dfs(int index, int sumW, int sumC)
{if (index == n)
    {if (sumW<= v)
        {maxvalue = max(maxvalue, sumC);
        }
        return;
    }
    dfs(index + 1, sumW, sumC);//不選第index個物品
    dfs(index + 1, sumW + w[index], sumC + c[index]);//選第index個物品
}

int main()
{cin >>n >>v;
    for (int i = 0; i< n; i++)
    {cin >>w[i] >>c[i];
    }
    dfs(0, 0, 0);//開始時對第1件物品進行選擇，此時背包重量0價值也是0
    cout<< maxvalue<< endl;
    return 0;
}

當(dāng)然了01背包問題如果用DFS來解決的話，當(dāng)數(shù)據(jù)比較大時，是不能AC的。這道題會超出時間限制。即便經(jīng)過剪枝也是無能為力的。

3.回溯——[USACO1.5]八皇后 Checker Challenge

題目鏈接


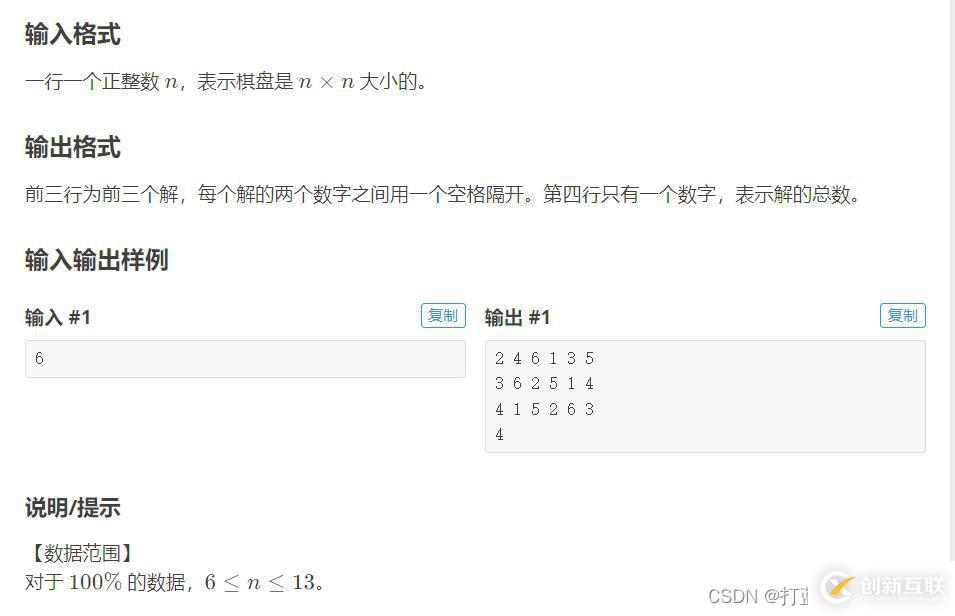
題目分析

八皇后問題是學(xué)習(xí)回溯很經(jīng)典的例題，這道題是八皇后問題的擴展，N皇后問題。也就是棋盤的大小是任意的。

這道題DFS的思路還是比較清晰的，每行有且只有一個棋子，那么DFS可以記錄下當(dāng)前處理的是第幾行的棋子。假設(shè)當(dāng)前處理的是第i行的棋子，那么要枚舉處在該行的棋子位置，判斷哪個是合法的。
什么樣的位置算是合法的呢，這個位置的列還有左對角線，右對角線位置都不能有棋子。那么又該如何表示這些位置呢？我們采用一維數(shù)組來分別表示列，左對角線，右對角線。列很好表示就是b[j]，左對角線我們可以發(fā)現(xiàn)行減去列的絕對值是恒定的，即c[i-j+n],右對角線行加列是恒定的。即d[i+j]。

小伙伴們可以自己畫畫圖看一看噢~

當(dāng)某位置放置了棋子，那么就將和它同列同對角線的位置都取為1，即b[j]=1,c[i-j+n]=1,d[i+j]=1。

AC代碼

#includeusing namespace std;

int a[100], b[100], c[100], d[100];//a[]儲存解b列c左斜d右斜
int n;//棋盤大小
int ans;

bool check(int i, int j)//檢查(i,j)是否合法
{if (!b[j] && !c[j - i + n] && !d[j + i]) return true;//b[j],c[i-j+n],d[i+j]為0說明該點可以放置棋子。
    return false;
}

void dfs(int i)//dfs第i行棋子
{//邊界條件
    if (i >n)//dfs完所有的棋子
    { 	ans++;
        if (ans<= 3)//只要前三個解
        {for (int i = 1; i<= n; i++)//輸出解
            {cout<< a[i]<< ' ';
                
            }
            cout<< endl;  
        }
        return;     
    }
    
        for (int j = 1; j<= n; j++)//枚舉一行的所有位置
        {//(i,j)點滿足放棋子的條件，我們就把棋子放在(i,j)點
            if (check(i, j))
            {a[i] = j;//把滿足解的列號存在a[i]中
                b[j] = 1;//修改現(xiàn)場
                c[ j - i + n] = 1;
                d[j + i] = 1;
                dfs(i + 1);//處理下一行的棋子
                b[j] = 0;//回溯，恢復(fù)現(xiàn)場
                c[j - i + n] = 0;
                d[j + i] = 0;
            }
        }
}
int main()
{cin >>n;
    dfs(1);
    cout<< ans<< endl;
    return 0;
}

4.遞歸實現(xiàn)排列型枚舉

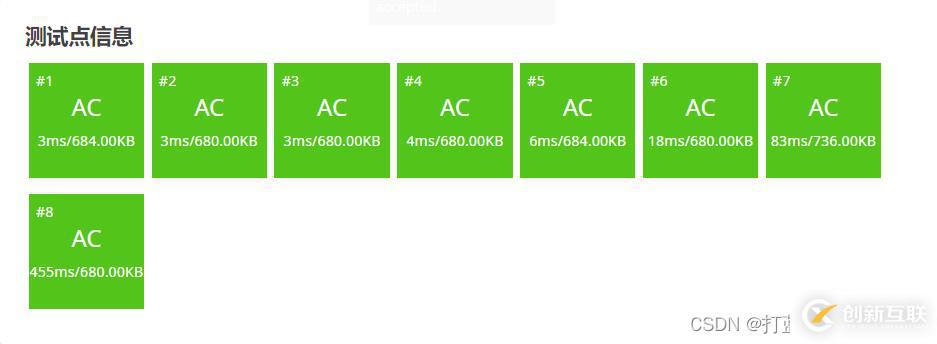
題目鏈接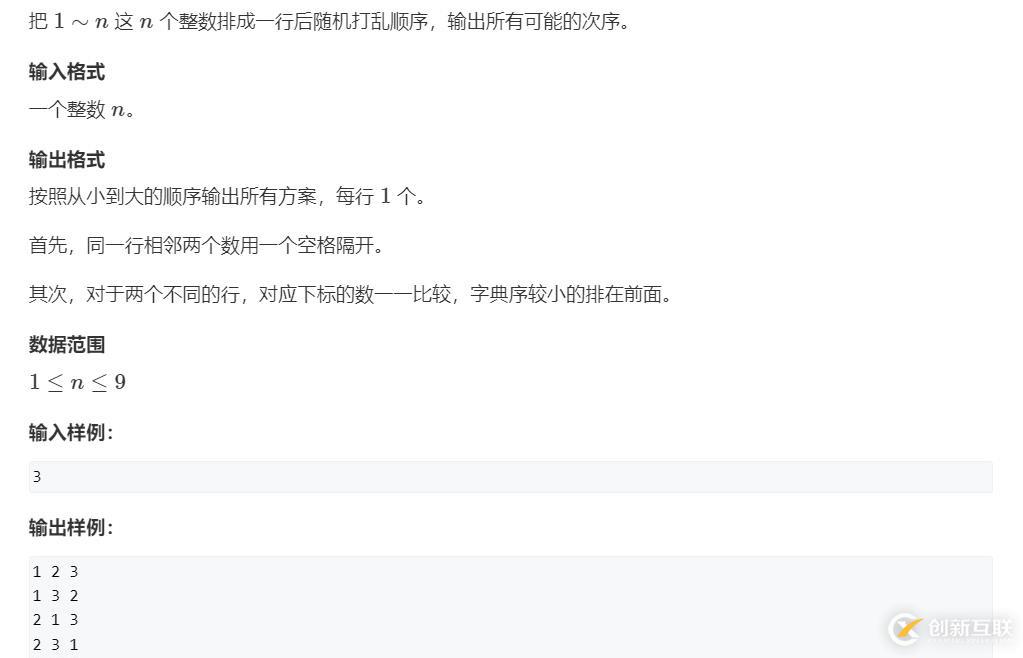

題目分析

DFS可以用來處理排列組合問題。

對于全排列問題我們可以這樣想，第1個位置可以放1~n任意一個數(shù)，第2個位置可以放除了放在第1個位置的數(shù)以外的任何一個數(shù)，以此類推。因此我們可以畫出一個遞歸搜索樹，用map[]來表示儲存當(dāng)前排列。DFS函數(shù)要記住當(dāng)前處理的是第index個位置，從1到n進行遍歷，看看這個數(shù)是否可以放在第index個位置，需要有一個判重數(shù)組hashtable[x]來記錄x是否在排列里面。

AC代碼

#includeusing namespace std;

const int N = 11;
//map[N]儲存當(dāng)前的排列，hashtable[N]判斷某個數(shù)是否在排列里
int map[N];
bool hashtable[N];面。
int n;

void dfs(int index)//當(dāng)前填第index位置
{if (index == n + 1)//已經(jīng)處理完1~n個位置
    {for (int i = 1; i<= n; i++)//輸出當(dāng)前排列
        {cout<< map[i]<< ' ';
        }
        cout<< endl;
        return;
    }
    for (int i = 1; i<= n; i++)//枚舉1~n
    {if (hashtable[i] == false)//當(dāng)i這個數(shù)沒有填在map中
        {map[index] = i;//第index位置填入i這個數(shù)
            hashtable[i] = true;//記i在當(dāng)前排列
            dfs(index + 1);//處理第index+1位置
            //處理完map[index]=i的子問題，恢復(fù)現(xiàn)場
            hashtable[i] = false;
            map[index] = 0;
        }
    }
}
int main()
{cin >>n;
    dfs(1);//從1這個數(shù)開始搜索
    return 0;
}

5.遞歸實現(xiàn)組合型枚舉

題目鏈接


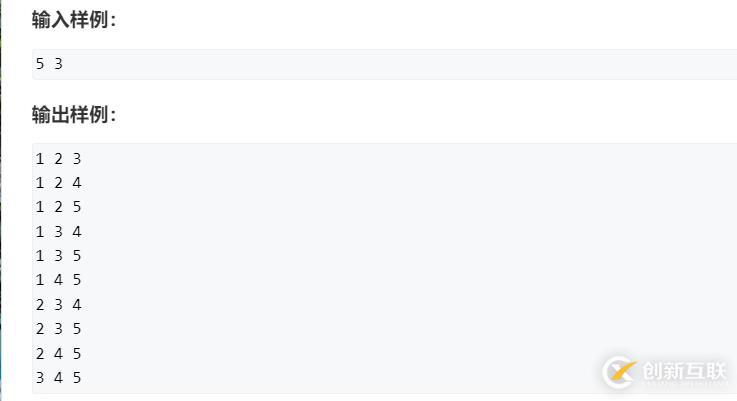
題目分析
組合和排列的大區(qū)別就是組合不需要考慮順序，也就是說123和132是一樣的。
由于題目要求同一行的數(shù)必須按升序排序，因此可以讓DFS函數(shù)記錄當(dāng)前處理的第index個位置，可以選的最小數(shù)start。

雖然參數(shù)變成了兩個，但是不需要判重數(shù)組了。

DFS的思路是這個樣子的，假設(shè)當(dāng)前處理的是第index個位置，這個位置可以放置start~n其中任意一個數(shù)。接著處理第index+1個位置，這個位置可以放置的最小數(shù)是前一位數(shù)的下一個數(shù)。即i+1~n。

AC代碼

#includeusing namespace std;

const int N = 30;

int map[N];//存儲解
int n, m;
//dfs記錄當(dāng)前處理的第index個位置，可以選的最小數(shù)start
void dfs(int index, int start)
{if (index >m)//m個位置都處理完了
    {for (int i = 1; i<= m; i++)//輸出方案
        {cout<< map[i]<< " ";
        }
        cout<< endl;
        return;
    }
    //第index個位置可以選擇start~n里面的數(shù)
    for (int i = start; i<= n; i++)
    {map[index] = i;
        //處理index+1位置，能選擇的最小數(shù)是前面選擇的數(shù)+1
        dfs(index + 1, i + 1);
        //處理完第index位置放置i這個數(shù)的子問題后回溯。
        map[index] = 0;
      
    }
}

int main()
{cin >>n >>m;
    dfs(1, 1);
    return 0;
}

---

四、剪枝思想

前面也提到過剪枝的概念，現(xiàn)在詳細說下剪枝這種東西。我們知道DFS時間復(fù)雜度是很高的，如果不進行一些優(yōu)化的話，在數(shù)據(jù)很大的情況下很容易就爆TLE。這個時候我們就可以用剪枝這種東西來優(yōu)化啦~
在進行DFS的過程中對某條可以確定不存在解的分支采用直接剪短的策略。這樣會大大降低計算量。一個搜索樹剪掉一些分支就形象的叫它剪枝了。
剪枝一般都是利用題目的限制條件來確定哪些分支是不可能存在解的。

---

五、剪枝思想在DFS中的應(yīng)用

小伙伴們來回憶下01背包問題，我們是在選擇完所有物品后才進行判斷，看看背包總體積是否超過背包容量。是不是可以在選擇的過程中就加入這一判斷，這樣就可以減少很多的計算量。當(dāng)選第index件物品時，如果選上它那么背包的總體積就超出背包容量，我們一定不能選了。此時選第index件物品的分支就不可能存在解，直接剪掉。

//DFS維護三個參數(shù)，正在選第index個物品，當(dāng)前的總體積，當(dāng)前的總價值
void dfs(int index, int sumW, int sumC)
{if (index == n)//選擇完所有的物品，最終的sumW一定不大于v
    {maxvalue = max(maxvalue, sumC);
        return;
    }
    dfs(index + 1, sumW, sumC);//不選第index個物品
    if (sum + w[index]<= v)//剪枝
    {//選第index個物品
    	dfs(index + 1, sumW + w[index], sumC + c[index]);
    } 
}

小伙伴們再來回憶下前面的組合型枚舉問題，我們也可以用到剪枝來優(yōu)化。可以看出要是剩下的數(shù)全都用上也滿足不了一共m個數(shù)的要求，那么我們直接可以結(jié)束這個分支了。即n - start + index< m。

void dfs(int index, int start)
{if (n - start + index< m) return;//剪枝
    if (index >m)//m個位置都處理完了
    {for (int i = 1; i<= m; i++)//輸出方案
        {cout<< map[i]<< " ";
        }
        cout<< endl;
        return;
    }
    //第index個位置可以選擇start~n里面的數(shù)
    for (int i = start; i<= n; i++)
    {map[index] = i;
        //處理index+1位置，能選擇的最小數(shù)是前面選擇的數(shù)+1
        dfs(index + 1, i + 1);
        //處理完第index位置放置i這個數(shù)的子問題后回溯。
        map[index] = 0;
      
    }
}

通過下表我們能看出剪枝之后的運行速度確實快了不少。

---

寫在后面

想到啥就說啥了，給備戰(zhàn)藍橋杯的小伙伴們提些建議。

我不推薦大家去leetcode上刷題，因為leetcode的形式和藍橋杯是不太一樣的。力扣只需要寫函數(shù)，輸入輸出已經(jīng)內(nèi)置好了。藍橋杯的輸入輸出是需要自己寫的。另外呢力扣主要是面向找工作的，題目是面試用的，不是專門打比賽的。因此題目不太適合藍橋杯競賽。當(dāng)然了里面的題目還是很經(jīng)典的，專門學(xué)某一算法是可以刷力扣的。我給大家推薦幾個適合的網(wǎng)站還有書籍。

ACwing網(wǎng)站
洛谷
C語言網(wǎng)藍橋杯題庫
藍橋杯練習(xí)系統(tǒng)
藍橋杯官網(wǎng)題庫

這幾個網(wǎng)站和書是我一直在用的，真心推薦給大家~

美好的時光總是短暫的，又到了說再見的時候啦~一鍵三連支持一下吧！

你是否還在尋找穩(wěn)定的海外服務(wù)器提供商？創(chuàng)新互聯(lián)www.cdcxhl.cn海外機房具備T級流量清洗系統(tǒng)配攻擊溯源，準確流量調(diào)度確保服務(wù)器高可用性，企業(yè)級服務(wù)器適合批量采購，新人活動首月15元起，快前往官網(wǎng)查看詳情吧

新聞標題：【一萬字】藍橋杯算法競賽備考（一）——搜索專題（上）（C++）-創(chuàng)新互聯(lián)
轉(zhuǎn)載來源：http://chinadenli.net/article6/eohig.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供商城網(wǎng)站、軟件開發(fā)、網(wǎng)站維護、虛擬主機、品牌網(wǎng)站設(shè)計、網(wǎng)站改版

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)