canvas小畫板之平滑曲線的實(shí)現(xiàn)案例-創(chuàng)新互聯(lián)

小編給大家分享一下canvas小畫板之平滑曲線的實(shí)現(xiàn)案例，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

10年積累的成都網(wǎng)站設(shè)計(jì)、網(wǎng)站制作、外貿(mào)營銷網(wǎng)站建設(shè)經(jīng)驗(yàn)，可以快速應(yīng)對(duì)客戶對(duì)網(wǎng)站的新想法和需求。提供各種問題對(duì)應(yīng)的解決方案。讓選擇我們的客戶得到更好、更有力的網(wǎng)絡(luò)服務(wù)。我雖然不認(rèn)識(shí)你，你也不認(rèn)識(shí)我。但先做網(wǎng)站后付款的網(wǎng)站建設(shè)流程，更有衛(wèi)濱免費(fèi)網(wǎng)站建設(shè)讓你可以放心的選擇與我們合作。

功能需求

項(xiàng)目需求：需要實(shí)現(xiàn)一個(gè)可以自由書寫的小畫板

簡單實(shí)現(xiàn)

對(duì)于熟悉canvas的同學(xué)來說，這個(gè)需求很簡單，大致邏輯如下：

1）監(jiān)聽事件pointerdown，pointermove，pointerup

2）標(biāo)記是否拖拽畫線模式變量 isDrawing，在down事件時(shí)置為true，up的時(shí)候置為false

3）使用canvas的api，設(shè)置線條樣式，調(diào)用繪制線條接口lineTo方法

短短幾十行代碼就能實(shí)現(xiàn)：

<!doctype html>
<html>

<head>
    <meta charset=utf-8>
    <style>
        canvas {
            border: 1px solid #ccc
        }

        body {
            margin: 0;
        }
    </style>
</head>

<body style="overflow: hidden;background-color: rgb(250, 250, 250);touch-action: none;">
    <canvas id="c" width="1920" height="1080"></canvas>
    <script>
        var el = document.getElementById('c');
        var ctx = el.getContext('2d');
        //設(shè)置繪制線條樣式
        ctx.strokeStyle = 'red';
        ctx.lineWidth = 1;
        ctx.lineJoin = 'round';
        ctx.lineCap = 'round';
        var isDrawing;//標(biāo)記是否要繪制
        //存儲(chǔ)坐標(biāo)點(diǎn)
        let lastX, lastY;
        document.body.onpointerdown = function (e) {
            console.log('pointerdown');
            isDrawing = true;
            lastX = e.clientX;
            lastY = e.clientY;
        };
        document.body.onpointermove = function (e) {
            console.log('pointermove');
            if (isDrawing) {
                draw(e.clientX, e.clientY, lastX, lastY);
            }
            lastX = e.clientX, lastY = e.clientY;
        };
        document.body.onpointerup = function (e) {
            if (isDrawing) {
                draw(e.clientX, e.clientY, lastX, lastY);
            }
            lastX = e.clientX, lastY = e.clientY;
            isDrawing = false;
        };

        function draw(x, y, lastX, lastY) {
            ctx.beginPath();
            ctx.moveTo(lastX, lastY);
            ctx.lineTo(x, y);
            ctx.stroke();
        }
    </script>
</body>
</html>

實(shí)現(xiàn)效果如下圖：

canvas小畫板之平滑曲線的實(shí)現(xiàn)案例

以上就簡單的實(shí)現(xiàn)了畫板功能，如果要求不高的用戶可以使用，但一旦遇到有點(diǎn)要求的用戶就無法交付這種產(chǎn)品，仔細(xì)看是線條折線感太強(qiáng)。

為什么會(huì)有折線感呢？

主要原因：

我們調(diào)用的api方法lineTo是兩點(diǎn)連線也就是直線

瀏覽器對(duì)鼠標(biāo)事件mousemove的采集是有采集頻率的，并不是每個(gè)鼠標(biāo)移動(dòng)經(jīng)過的每一個(gè)像素點(diǎn)都會(huì)觸發(fā)事件。

當(dāng)鼠標(biāo)移動(dòng)的越快，那么兩點(diǎn)之間的間隔就越遠(yuǎn)，那么折線感就更明顯。

canvas小畫板之平滑曲線的實(shí)現(xiàn)案例

如何能繪制平滑的曲線？

canvas提供的api中是有現(xiàn)成接口的，貝塞爾系列的接口就能滿足我們的要求，接下來我們講一下使用二次貝塞爾曲線繪制平滑曲線。

quadraticCurveTo(cpx,cpy,x,y)

二次貝塞爾曲線接口需要四個(gè)參數(shù)，cpx，cpy是曲線的控制點(diǎn)，x，y是曲線終點(diǎn)。

有人問那曲線的起點(diǎn)在哪里？其實(shí)曲線的起點(diǎn)取決于上一操作狀態(tài)，可以是moveTo的位置，或者是lineTo的位置，或者是貝塞爾的終點(diǎn)。

那么怎么調(diào)用quadraticCurveTo，參數(shù)怎么傳呢？

我們需要找出關(guān)鍵位置，直接用例子告訴大家吧

1）假如我們用鼠標(biāo)采集到ABCDEF六個(gè)點(diǎn)

2）取前面三個(gè)點(diǎn)ABC計(jì)算，BC的中點(diǎn)B1，以A為起點(diǎn)，B為控制點(diǎn)，B1為終點(diǎn)，那么利用quadraticCurveTo可以繪制出這樣一條貝塞爾曲線

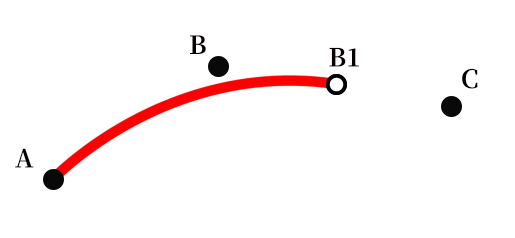
canvas小畫板之平滑曲線的實(shí)現(xiàn)案例

3）接下來計(jì)算CD的中點(diǎn)C1，以B1為起點(diǎn)，C為控制點(diǎn)，C1為終點(diǎn)，那么利用quadraticCurveTo可以繪制出這樣一條貝塞爾曲線

canvas小畫板之平滑曲線的實(shí)現(xiàn)案例

4）以此類推，當(dāng)?shù)搅俗詈笠粋€(gè)點(diǎn)時(shí)以D1為起點(diǎn)，E為控制點(diǎn)，F(xiàn)為終點(diǎn)，結(jié)束貝塞爾繪制。

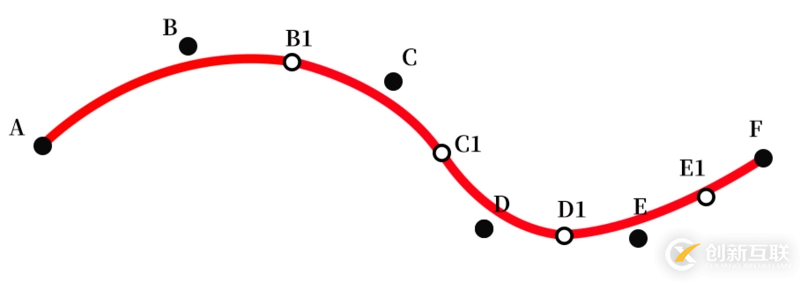
canvas小畫板之平滑曲線的實(shí)現(xiàn)案例

根據(jù)算法進(jìn)行代碼改造

OK我們介紹了具體算法的影響，那用該算法對(duì)我們前面的代碼進(jìn)行改造：

<!doctype html>
<html>

<head>
    <meta charset=utf-8>
    <style>
        canvas {
            border: 1px solid #ccc
        }

        body {
            margin: 0;
        }
    </style>
</head>

<body style="overflow: hidden;background-color: rgb(250, 250, 250);touch-action: none;">
    <canvas id="c" width="1920" height="1080"></canvas>
    <script>
        var el = document.getElementById('c');
        var ctx = el.getContext('2d');
        //設(shè)置繪制線條樣式
        ctx.strokeStyle = 'red';
        ctx.lineWidth = 1;
        ctx.lineJoin = 'round';
        ctx.lineCap = 'round';
        var isDrawing;//標(biāo)記是否要繪制
        //存儲(chǔ)坐標(biāo)點(diǎn)
        let points = [];
        document.body.onpointerdown = function (e) {
            console.log('pointerdown');
            isDrawing = true;
            points.push({ x: e.clientX, y: e.clientY });
        };
        document.body.onpointermove = function (e) {
            console.log('pointermove');
            if (isDrawing) {
                draw(e.clientX, e.clientY);
            }

        };
        document.body.onpointerup = function (e) {
            if (isDrawing) {
                draw(e.clientX, e.clientY);
            }
            points = [];
            isDrawing = false;
        };

        function draw(mousex, mousey) {
            points.push({ x: mousex, y: mousey });
            ctx.beginPath();
            let x = (points[points.length - 2].x + points[points.length - 1].x) / 2,
                y = (points[points.length - 2].y + points[points.length - 1].y) / 2;
            if (points.length == 2) {
                ctx.moveTo(points[points.length - 2].x, points[points.length - 2].y);
                ctx.lineTo(x, y);
            } else {
                let lastX = (points[points.length - 3].x + points[points.length - 2].x) / 2,
                    lastY = (points[points.length - 3].y + points[points.length - 2].y) / 2;
                ctx.moveTo(lastX, lastY);
                ctx.quadraticCurveTo(points[points.length - 2].x, points[points.length - 2].y, x, y);
            }
            ctx.stroke();
            points.slice(0, 1);

        }
    </script>
</body>

</html>

在原有基礎(chǔ)上我們用了一個(gè)數(shù)組points保存鼠標(biāo)經(jīng)過的點(diǎn)，根據(jù)算法可知繪制貝塞爾曲線至少要用三個(gè)點(diǎn)，繪制過程中維護(hù)points數(shù)組。

實(shí)現(xiàn)效果如下，可見平滑了很多！

canvas小畫板之平滑曲線的實(shí)現(xiàn)案例

以上是“canvas小畫板之平滑曲線的實(shí)現(xiàn)案例”這篇文章的所有內(nèi)容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內(nèi)容對(duì)大家有所幫助，如果還想學(xué)習(xí)更多知識(shí)，歡迎關(guān)注創(chuàng)新互聯(lián)行業(yè)資訊頻道！

網(wǎng)站欄目：canvas小畫板之平滑曲線的實(shí)現(xiàn)案例-創(chuàng)新互聯(lián)
標(biāo)題URL：http://chinadenli.net/article6/ecoog.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供Google、App設(shè)計(jì)、外貿(mào)建站、網(wǎng)站設(shè)計(jì)公司、移動(dòng)網(wǎng)站建設(shè)、網(wǎng)站制作

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請(qǐng)盡快告知，我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng)，如需處理請(qǐng)聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時(shí)需注明來源：創(chuàng)新互聯(lián)

猜你還喜歡下面的內(nèi)容

欧美一区二区三区老妇人-欧美做爰猛烈大尺度电-99久久夜色精品国产亚洲a-亚洲福利视频一区二区

canvas小畫板之平滑曲線的實(shí)現(xiàn)案例-創(chuàng)新互聯(lián)