今天就跟大家聊聊有關(guān)Python中都有哪些排序算法，可能很多人都不太了解，為了讓大家更加了解，小編給大家總結(jié)了以下內(nèi)容，希望大家根據(jù)這篇文章可以有所收獲。

成都創(chuàng)新互聯(lián)公司于2013年成立，是專業(yè)互聯(lián)網(wǎng)技術(shù)服務(wù)公司，擁有項目成都做網(wǎng)站、網(wǎng)站建設(shè)網(wǎng)站策劃，項目實施與項目整合能力。我們以讓每一個夢想脫穎而出為使命，1280元日照做網(wǎng)站,已為上家服務(wù),為日照各地企業(yè)和個人服務(wù),聯(lián)系電話:18980820575

1.冒泡排序

冒泡排序是 CS  入門課程中最常講授的一種，因為它清楚地說明了排序的工作原理，同時又簡單又易于理解。冒泡排序?qū)⒅鸩奖闅v列表并比較相鄰的元素對。如果元素的順序錯誤，則會交換這些元素。重復(fù)對列表中未排序部分的遍歷，直到對列表進行排序。因為冒泡排序重復(fù)地通過列表中未排序的部分，所以它的最壞情況復(fù)雜性為O(n²)。

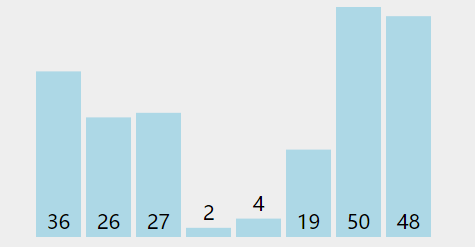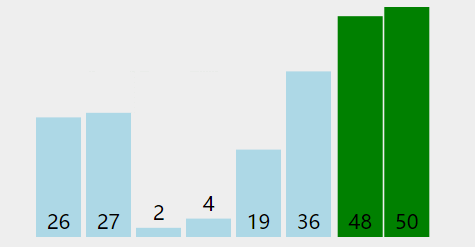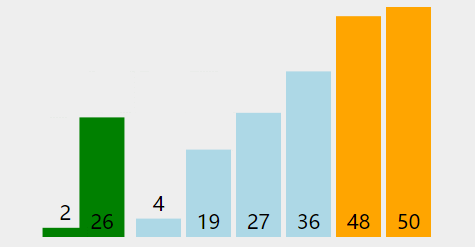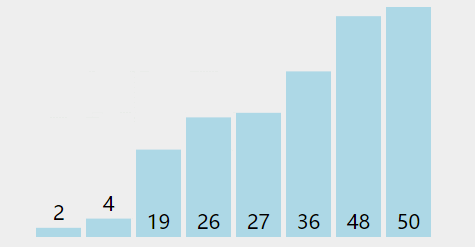
def bubble_sort(arr):     def swap(i, j):         arr[i], arr[j] = arr[j], arr[i]      n = len(arr)     swapped = True          x = -1     while swapped:         swapped = False         x = x + 1         for i in range(1, n-x):             if arr[i - 1] > arr[i]:                 swap(i - 1, i)                 swapped = True                          return arr

2.選擇排序

選擇排序也相當(dāng)簡單，優(yōu)于冒泡排序。如果你要在這兩者之間進行選擇，那么最好使用默認的“右選擇排序”。使用選擇排序，我們將輸入列表/數(shù)組分為兩部分：已排序項的子列表和構(gòu)成列表其余部分的剩余項的子列表。

我們首先在未排序的子列表中找到最小的元素，并將其放在已排序子列表的末尾。因此，我們不斷地獲取最小的未排序元素，并將其按排序順序放入已排序的子列表中。此過程將重復(fù)進行，直到列表完全排序。

def selection_sort(arr):             for i in range(len(arr)):         minimum = i                  for j in range(i + 1, len(arr)):             # 選擇最小值             if arr[j] < arr[minimum]:                 minimum = j          # 把它放在已排序的數(shù)組結(jié)尾         arr[minimum], arr[i] = arr[i], arr[minimum]                  return arr

3.插入排序

插入排序比冒泡排序和選擇排序都要快，而且可以說更加簡單。就像在玩紙牌游戲時，洗牌的過程就是反復(fù)進行插入排序!在每次循環(huán)迭代中，插入排序從數(shù)組中刪除一個元素。然后在另一個排序數(shù)組中查找該元素所屬的位置，并將其插入其中。它重復(fù)這個過程，直到?jīng)]有輸入元素保留。

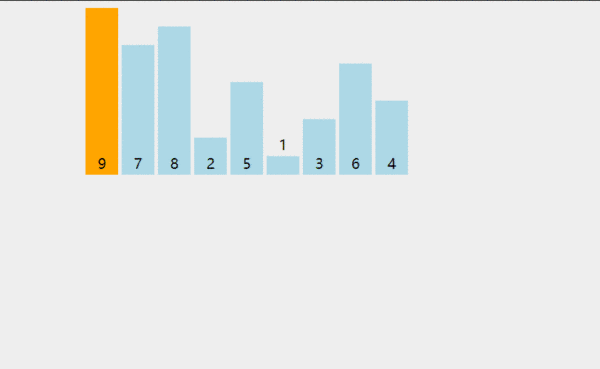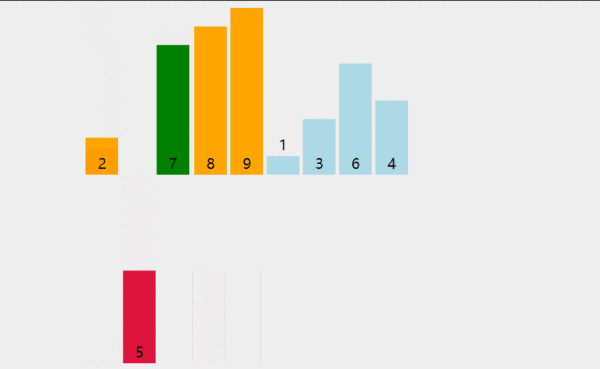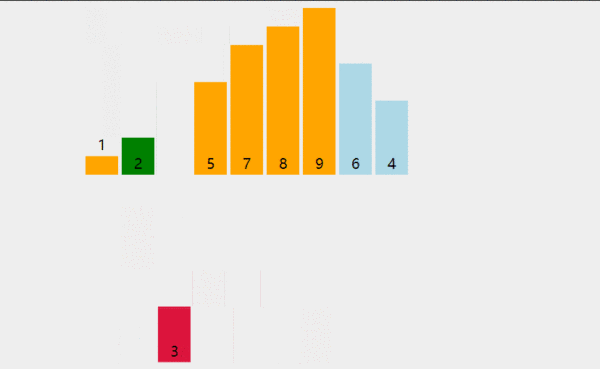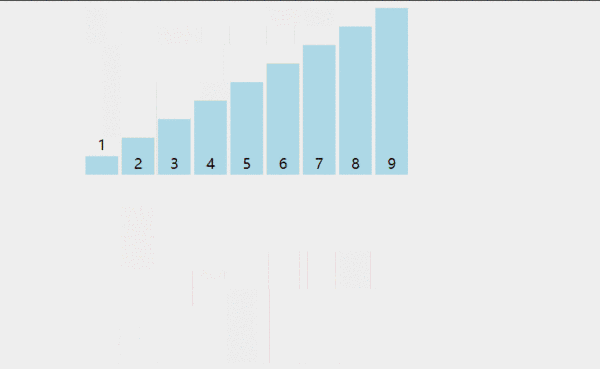
def insertion_sort(arr):              for i in range(len(arr)):         cursor = arr[i]         pos = i                  while pos > 0 and arr[pos - 1] > cursor:             # 交換列表中的數(shù)字             arr[pos] = arr[pos - 1]             pos = pos - 1         # 中斷并進行最終交換         arr[pos] = cursor      return arr

4.合并排序

合并排序是一個完美的分而治之的算法例子。使用這種算法只需要通過以下兩個主要步驟：

(1) 連續(xù)分割未排序的列表，直到有N個子列表，其中每個子列表都有1個“未排序”的元素，N是原始數(shù)組中的元素數(shù)。

(2) 反復(fù)合并，即一次將兩個子列表合并在一起，生成新的已排序子列表，直到所有元素都完全合并到一個已排序的數(shù)組中。

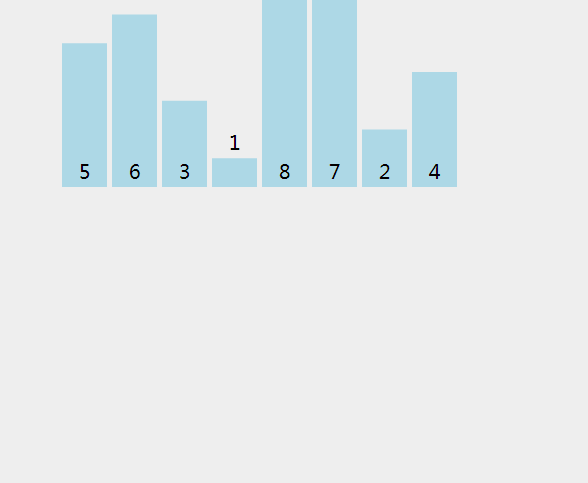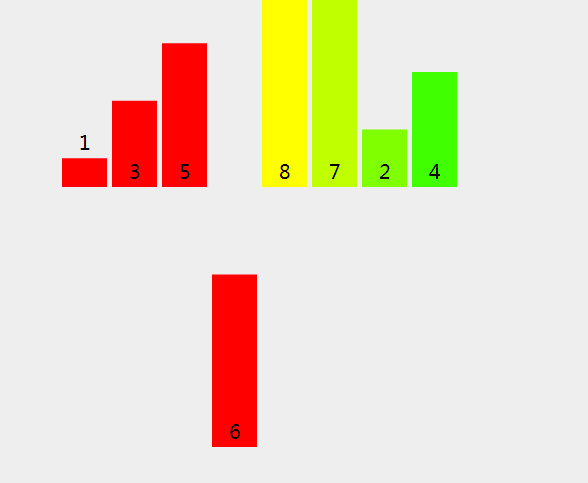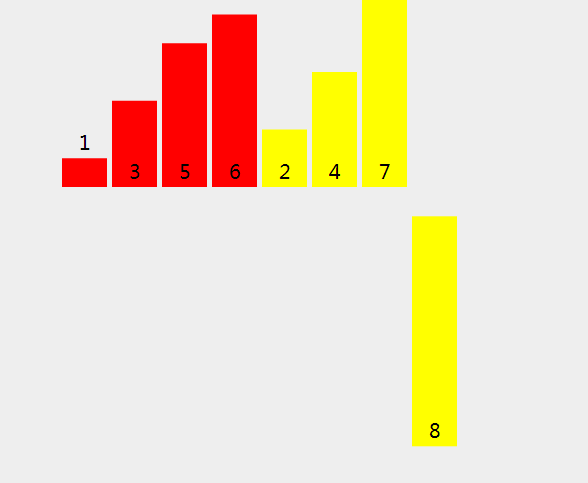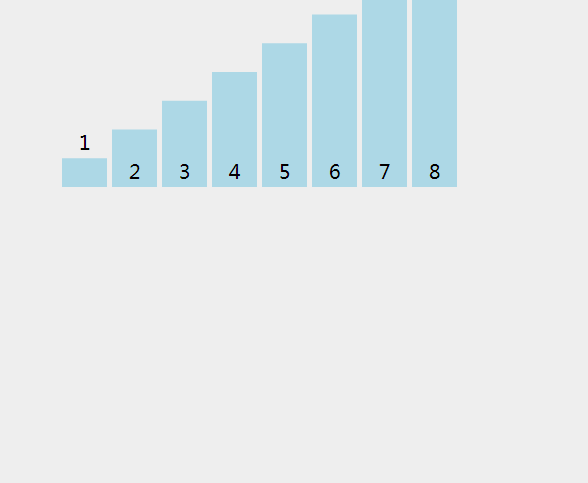
def merge_sort(arr):     # 對最后一個數(shù)組進行拆分     if len(arr) <= 1:         return arr     mid = len(arr) // 2     # 在兩個部分上遞歸執(zhí)行merge_sort     left, right = merge_sort(arr[:mid]), merge_sort(arr[mid:])      # 合并在一起     return merge(left, right, arr.copy())   def merge(left, right, merged):      left_cursor, right_cursor = 0, 0     while left_cursor < len(left) and right_cursor < len(right):                # 將每一個排序并放入結(jié)果         if left[left_cursor] <= right[right_cursor]:             merged[left_cursor+right_cursor]=left[left_cursor]             left_cursor += 1         else:             merged[left_cursor + right_cursor] = right[right_cursor]             right_cursor += 1                  for left_cursor in range(left_cursor, len(left)):         merged[left_cursor + right_cursor] = left[left_cursor]              for right_cursor in range(right_cursor, len(right)):         merged[left_cursor + right_cursor] = right[right_cursor]      return merged

5.快速排序

快速排序也是一種分而治之的算法，與合并排序一樣。盡管它有點復(fù)雜，但在大多數(shù)標(biāo)準(zhǔn)實現(xiàn)中，它的執(zhí)行速度比合并排序快得多，而且很少達到O(n²)的最壞情況復(fù)雜度。它有三個主要步驟：

(1) 我們首先從數(shù)組中選擇一個元素，稱之為pivot。

(2) 將小于軸的所有元素移到軸的左側(cè);將大于軸的所有元素移到軸的右側(cè)。這稱為分區(qū)操作。

(3) 遞歸地將上述2個步驟分別應(yīng)用于元素的每個子數(shù)組，這些元素的值比上一個軸的值小或大。

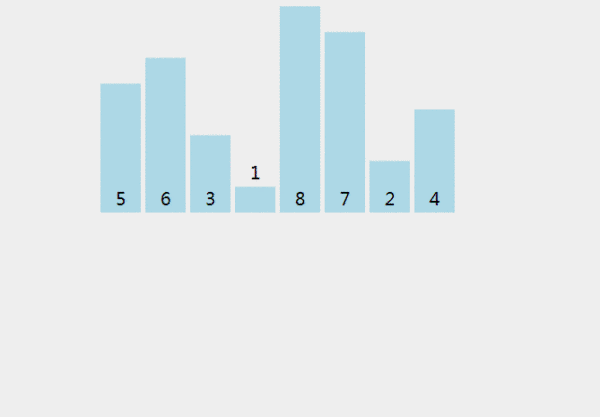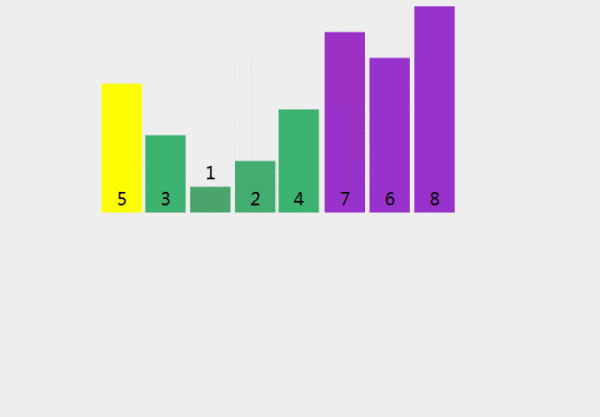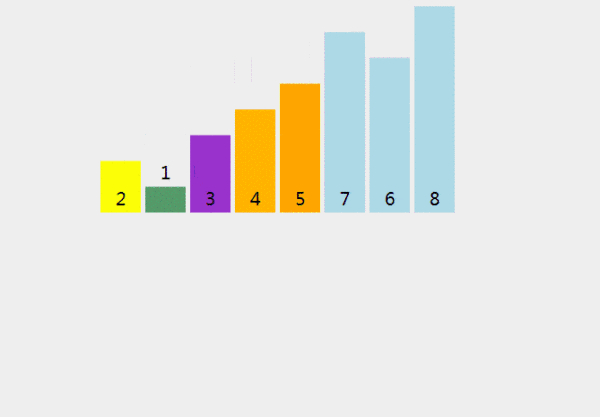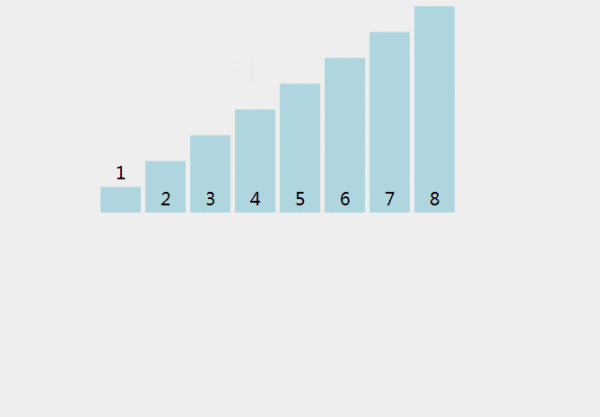
def partition(array, begin, end):     pivot_idx = begin     for i in xrange(begin+1, end+1):         if array[i] <= array[begin]:             pivot_idx += 1             array[i], array[pivot_idx] = array[pivot_idx], array[i]     array[pivot_idx], array[begin] = array[begin], array[pivot_idx]     return pivot_idx  def quick_sort_recursion(array, begin, end):     if begin >= end:         return     pivot_idx = partition(array, begin, end)     quick_sort_recursion(array, begin, pivot_idx-1)     quick_sort_recursion(array, pivot_idx+1, end)  def quick_sort(array, begin=0, end=None):     if end is None:         end = len(array) - 1          return quick_sort_recursion(array, begin, end)

看完上述內(nèi)容，你們對Python中都有哪些排序算法有進一步的了解嗎？如果還想了解更多知識或者相關(guān)內(nèi)容，請關(guān)注創(chuàng)新互聯(lián)行業(yè)資訊頻道，感謝大家的支持。

網(wǎng)頁標(biāo)題：Python中都有哪些排序算法
當(dāng)前路徑：http://chinadenli.net/article38/gghcsp.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供面包屑導(dǎo)航、動態(tài)網(wǎng)站、、Google、ChatGPT、靜態(tài)網(wǎng)站

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)