創(chuàng)新互聯(lián)www.cdcxhl.cn八線動(dòng)態(tài)BGP香港云服務(wù)器提供商，新人活動(dòng)買(mǎi)多久送多久，劃算不套路！

10年積累的成都網(wǎng)站建設(shè)、成都做網(wǎng)站經(jīng)驗(yàn)，可以快速應(yīng)對(duì)客戶對(duì)網(wǎng)站的新想法和需求。提供各種問(wèn)題對(duì)應(yīng)的解決方案。讓選擇我們的客戶得到更好、更有力的網(wǎng)絡(luò)服務(wù)。我雖然不認(rèn)識(shí)你，你也不認(rèn)識(shí)我。但先網(wǎng)站設(shè)計(jì)制作后付款的網(wǎng)站建設(shè)流程，更有濮陽(yáng)縣免費(fèi)網(wǎng)站建設(shè)讓你可以放心的選擇與我們合作。

這期內(nèi)容當(dāng)中小編將會(huì)給大家?guī)?lái)有關(guān)什么是Python中的二叉排序樹(shù)和平衡二叉樹(shù)，文章內(nèi)容豐富且以專(zhuān)業(yè)的角度為大家分析和敘述，閱讀完這篇文章希望大家可以有所收獲。

二叉排序樹(shù)

二叉排序樹(shù)又稱(chēng)為二叉查找樹(shù)。它或者是一顆空樹(shù)，或者是具有下列性質(zhì)的二叉樹(shù)：

若它的左子樹(shù)不為空，則左子樹(shù)上所有節(jié)點(diǎn)的值均小于它的根結(jié)構(gòu)的值；若它的右子樹(shù)不為空，則右子樹(shù)上所有節(jié)點(diǎn)的值均大于它的根結(jié)構(gòu)的值；它的左、右子樹(shù)也分別為二叉排序樹(shù)。

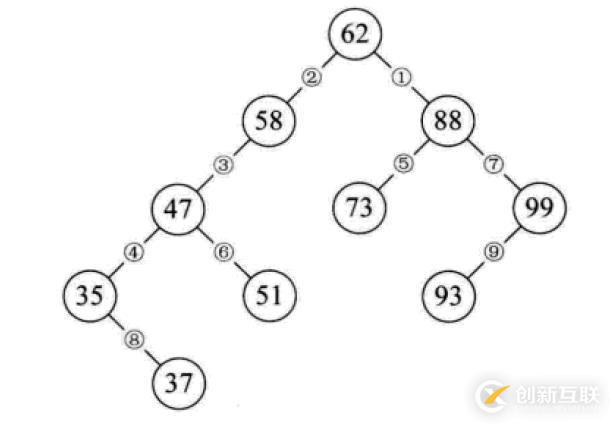
構(gòu)造一顆二叉排序樹(shù)的目的，往往不是為了排序，而是為了提高查找和插入刪除關(guān)鍵字的速度。

二叉排序樹(shù)的操作：

查找：對(duì)比節(jié)點(diǎn)的值和關(guān)鍵字，相等則表明找到了；小了則往節(jié)點(diǎn)的左子樹(shù)去找，大了則往右子樹(shù)去找，這么遞歸下去，最后返回布爾值或找到的節(jié)點(diǎn)。插入：從根節(jié)點(diǎn)開(kāi)始逐個(gè)與關(guān)鍵字進(jìn)行對(duì)比，小了去左邊，大了去右邊，碰到子樹(shù)為空的情況就將新的節(jié)點(diǎn)鏈接。刪除：如果要?jiǎng)h除的節(jié)點(diǎn)是葉子，直接刪；如果只有左子樹(shù)或只有右子樹(shù)，則刪除節(jié)點(diǎn)后，將子樹(shù)鏈接到父節(jié)點(diǎn)即可；如果同時(shí)有左右子樹(shù)，則可以將二叉排序樹(shù)進(jìn)行中序遍歷，取將要被刪除的節(jié)點(diǎn)的前驅(qū)或者后繼節(jié)點(diǎn)替代這個(gè)被刪除的節(jié)點(diǎn)的位置。

      """
    定義一個(gè)二叉樹(shù)節(jié)點(diǎn)類(lèi)。
    以討論算法為主，忽略了一些諸如對(duì)數(shù)據(jù)類(lèi)型進(jìn)行判斷的問(wèn)題。
    """
    def __init__(self, data, left=None, right=None):
        """
        初始化
        :param data: 節(jié)點(diǎn)儲(chǔ)存的數(shù)據(jù)
        :param left: 節(jié)點(diǎn)左子樹(shù)
        :param right: 節(jié)點(diǎn)右子樹(shù)
        """
        self.data = data
        self.left = left
        self.right = rightclass BinarySortTree:
    """
    基于BSTNode類(lèi)的二叉排序樹(shù)。維護(hù)一個(gè)根節(jié)點(diǎn)的指針。
    """
    def __init__(self):
        self._root = None
    def is_empty(self):
        return self._root is None
    def search(self, key):
        """
        關(guān)鍵碼檢索
        :param key: 關(guān)鍵碼
        :return: 查詢節(jié)點(diǎn)或None
        """
        bt = self._root        while bt:
            entry = bt.data            if key < entry:
                bt = bt.left            elif key > entry:
                bt = bt.right            else:                return entry        return None
    def insert(self, key):
        """
        插入操作
        :param key:關(guān)鍵碼 
        :return: 布爾值
        """
        bt = self._root        if not bt:
            self._root = BSTNode(key)            return
        while True:
            entry = bt.data            if key < entry:                if bt.left is None:
                    bt.left = BSTNode(key)                    return
                bt = bt.left            elif key > entry:                if bt.right is None:
                    bt.right = BSTNode(key)                    return
                bt = bt.right            else:
                bt.data = key                return
    def delete(self, key):
        """
        二叉排序樹(shù)最復(fù)雜的方法
        :param key: 關(guān)鍵碼
        :return: 布爾值
        """
        p, q = None, self._root     # 維持p為q的父節(jié)點(diǎn)，用于后面的鏈接操作
        if not q:
            print("空樹(shù)！")            return
        while q and q.data != key:
            p = q            if key < q.data:
                q = q.left            else:
                q = q.right            if not q:               # 當(dāng)樹(shù)中沒(méi)有關(guān)鍵碼key時(shí)，結(jié)束退出。
                return
        # 上面已將找到了要?jiǎng)h除的節(jié)點(diǎn)，用q引用。而p則是q的父節(jié)點(diǎn)或者None（q為根節(jié)點(diǎn)時(shí)）。
        if not q.left:            if p is None:
                self._root = q.right            elif q is p.left:
                p.left = q.right            else:
                p.right = q.right            return
        # 查找節(jié)點(diǎn)q的左子樹(shù)的最右節(jié)點(diǎn)，將q的右子樹(shù)鏈接為該節(jié)點(diǎn)的右子樹(shù)
        # 該方法可能會(huì)增大樹(shù)的深度，效率并不算高。可以設(shè)計(jì)其它的方法。
        r = q.left        while r.right:
            r = r.right
        r.right = q.right        if p is None:
            self._root = q.left        elif p.left is q:
            p.left = q.left        else:
            p.right = q.left    def __iter__(self):
        """
        實(shí)現(xiàn)二叉樹(shù)的中序遍歷算法,
        展示我們創(chuàng)建的二叉排序樹(shù).
        直接使用python內(nèi)置的列表作為一個(gè)棧。
        :return: data
        """
        stack = []
        node = self._root        while node or stack:            while node:
                stack.append(node)
                node = node.left
            node = stack.pop()            yield node.data
            node = node.rightif __name__ == '__main__':
    lis = [62, 58, 88, 48, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 50]
    bs_tree = BinarySortTree()    for i in range(len(lis)):
        bs_tree.insert(lis[i])    # bs_tree.insert(100)
    bs_tree.delete(58)    for i in bs_tree:
        print(i, end=" ")    # print("\n", bs_tree.search(4))

二叉排序樹(shù)總結(jié)：

二叉排序樹(shù)以鏈?zhǔn)竭M(jìn)行存儲(chǔ)，保持了鏈接結(jié)構(gòu)在插入和刪除操作上的優(yōu)點(diǎn)。在極端情況下，查詢次數(shù)為1，但大操作次數(shù)不會(huì)超過(guò)樹(shù)的深度。也就是說(shuō)，二叉排序樹(shù)的查找性能取決于二叉排序樹(shù)的形狀，也就引申出了后面的平衡二叉樹(shù)。給定一個(gè)元素集合，可以構(gòu)造不同的二叉排序樹(shù)，當(dāng)它同時(shí)是一個(gè)完全二叉樹(shù)的時(shí)候，查找的時(shí)間復(fù)雜度為O(log(n))，近似于二分查找。當(dāng)出現(xiàn)最極端的斜樹(shù)時(shí)，其時(shí)間復(fù)雜度為O(n)，等同于順序查找，效果最差。

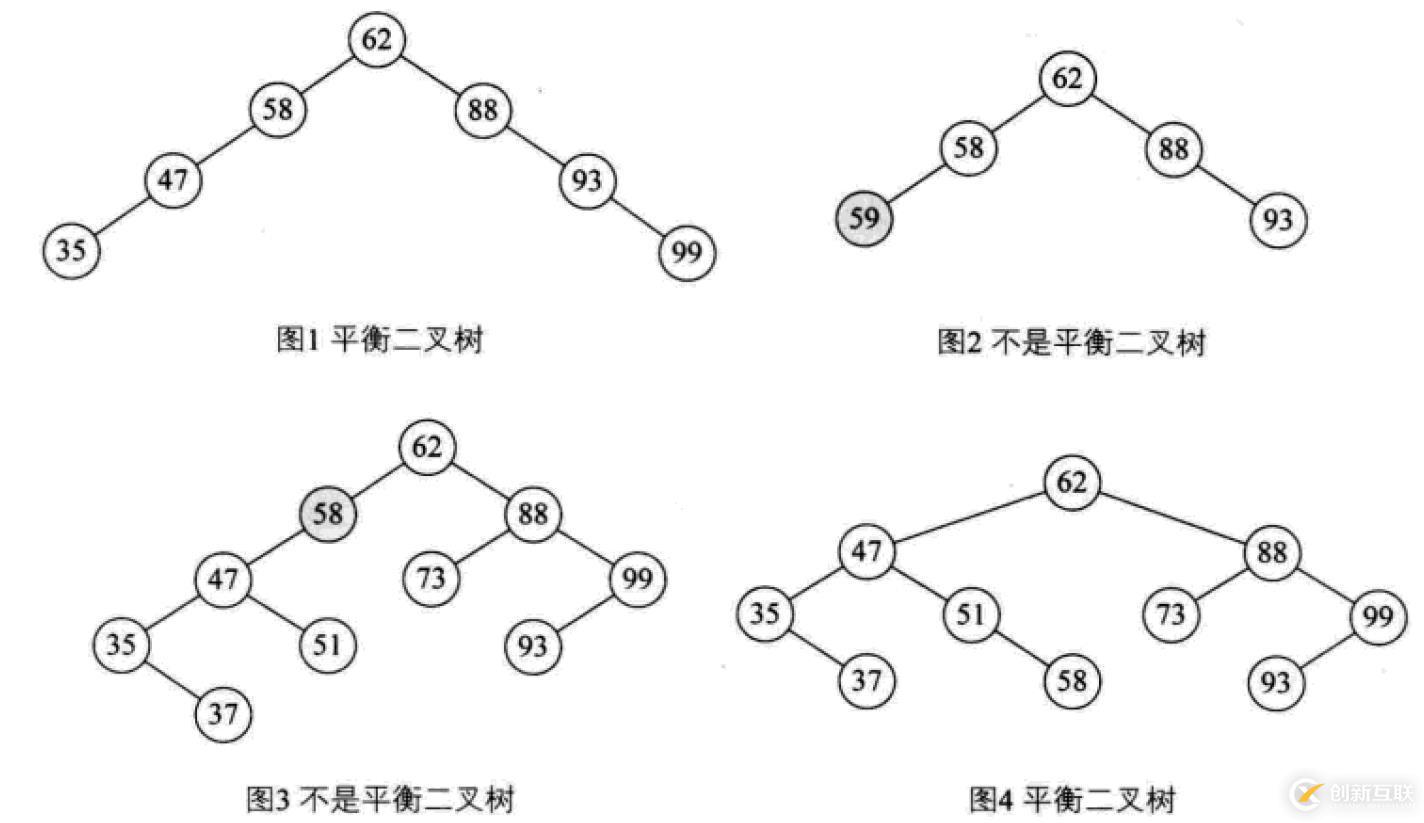
平衡二叉樹(shù)

平衡二叉樹(shù)（AVL樹(shù)，發(fā)明者的姓名縮寫(xiě)）：一種高度平衡的排序二叉樹(shù)，其每一個(gè)節(jié)點(diǎn)的左子樹(shù)和右子樹(shù)的高度差最多等于1。

平衡二叉樹(shù)首先必須是一棵二叉排序樹(shù)！

平衡因子（Balance Factor）：將二叉樹(shù)上節(jié)點(diǎn)的左子樹(shù)深度減去右子樹(shù)深度的值。

對(duì)于平衡二叉樹(shù)所有包括分支節(jié)點(diǎn)和葉節(jié)點(diǎn)的平衡因子只可能是-1,0和1，只要有一個(gè)節(jié)點(diǎn)的因子不在這三個(gè)值之內(nèi)，該二叉樹(shù)就是不平衡的。

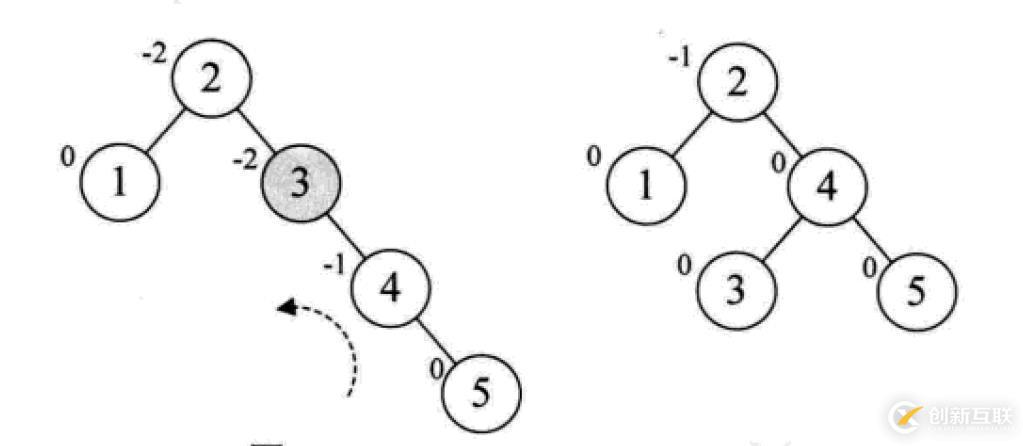
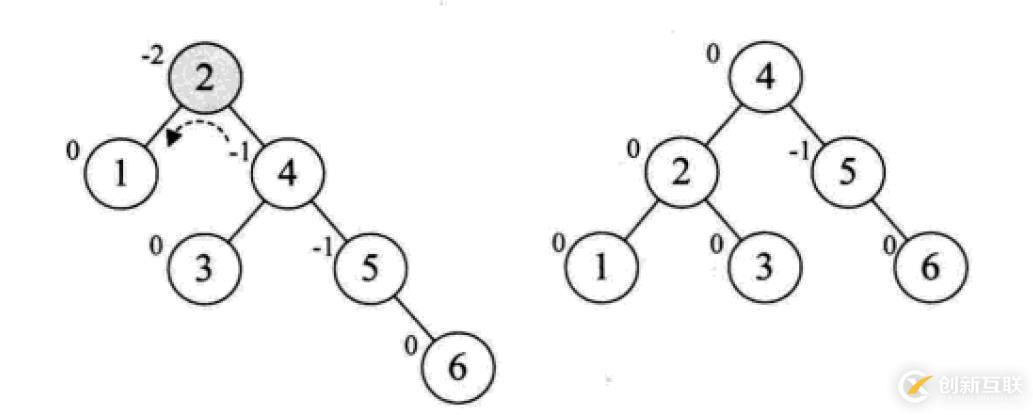
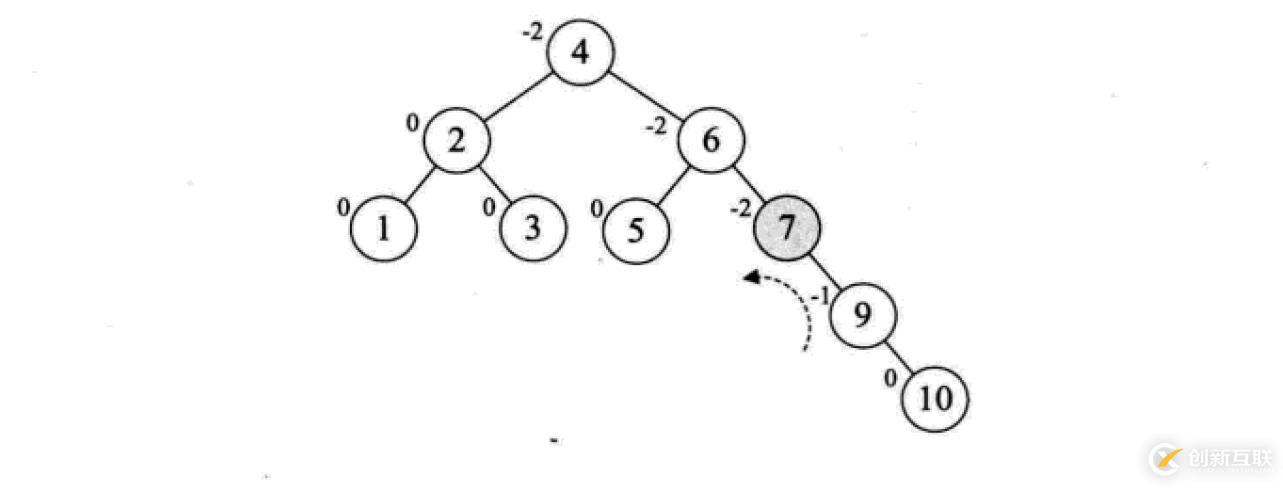
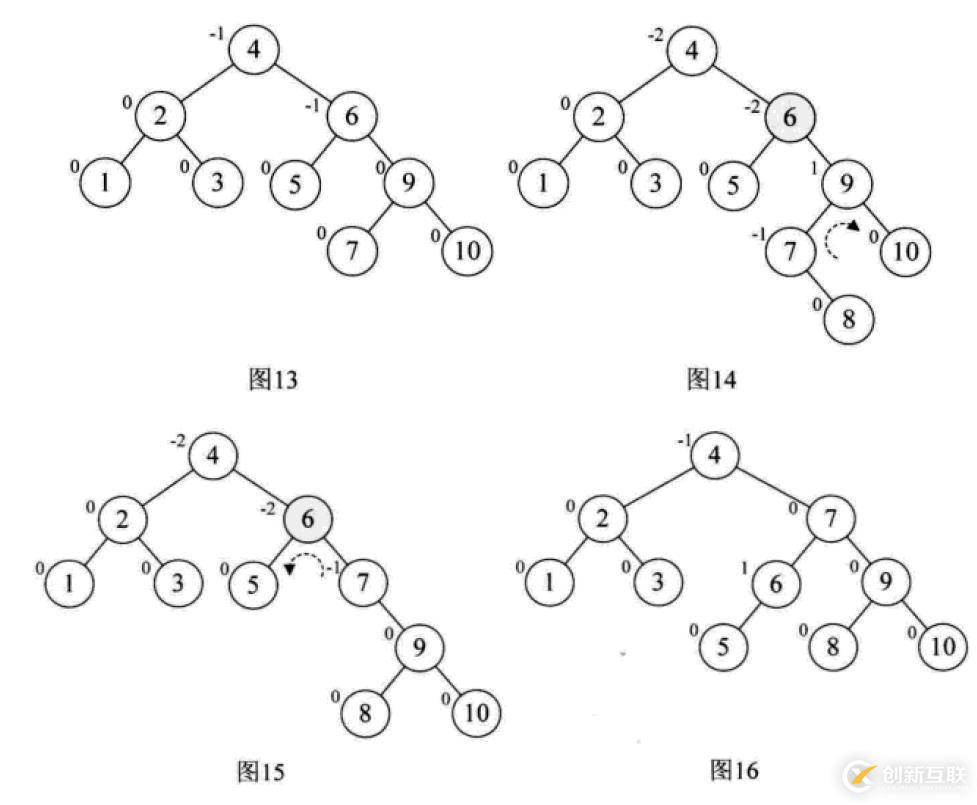
最小不平衡子樹(shù)：距離插入結(jié)點(diǎn)最近的，且平衡因子的絕對(duì)值大于1的節(jié)點(diǎn)為根的子樹(shù)。

平衡二叉樹(shù)的構(gòu)建思想：每當(dāng)插入一個(gè)新結(jié)點(diǎn)時(shí)，先檢查是否破壞了樹(shù)的平衡性，若有，找出最小不平衡子樹(shù)。在保持二叉排序樹(shù)特性的前提下，調(diào)整最小不平衡子樹(shù)中各結(jié)點(diǎn)之間的連接關(guān)系，進(jìn)行相應(yīng)的旋轉(zhuǎn)，成為新的平衡子樹(shù)。

下面是由[1,2,3,4,5,6,7,10,9]構(gòu)建平衡二叉樹(shù)

上述就是小編為大家分享的什么是Python中的二叉排序樹(shù)和平衡二叉樹(shù)了，如果剛好有類(lèi)似的疑惑，不妨參照上述分析進(jìn)行理解。如果想知道更多相關(guān)知識(shí)，歡迎關(guān)注創(chuàng)新互聯(lián)-成都網(wǎng)站建設(shè)公司行業(yè)資訊頻道。

網(wǎng)站標(biāo)題：什么是Python中的二叉排序樹(shù)和平衡二叉樹(shù)-創(chuàng)新互聯(lián)
當(dāng)前地址：http://chinadenli.net/article34/edhpe.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供ChatGPT、全網(wǎng)營(yíng)銷(xiāo)推廣、外貿(mào)建站、網(wǎng)站收錄、定制網(wǎng)站、微信公眾號(hào)

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請(qǐng)盡快告知，我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng)，如需處理請(qǐng)聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時(shí)需注明來(lái)源： 創(chuàng)新互聯(lián)