#include <assert.h>
#include <iostream>
using namespace std;
#include <stack>
#include <queue>

template<class T>
struct BinaryTreeNode
{
	BinaryTreeNode<T>* _left;
	BinaryTreeNode<T>* _right;
	T _data;

	BinaryTreeNode(const T& x)
		:_left(NULL)
		,_right(NULL)
		,_data(x)
	{}
};

template<class T>
class BinaryTree
{
public:
	BinaryTree()
		:_root(NULL)
	{}

	BinaryTree(const T* a, size_t size, const T& invalid)
	{
		size_t index = 0;
		_root = _CreateTree(a, size, index, invalid);
	}

	~BinaryTree()
	{
		_DestroyTree(_root);
		_root = NULL;
	}

	BinaryTree(const BinaryTree<T>& t)
	{
		_root = _CopyTree(t._root);
	}

	//賦值運算符重載的傳統(tǒng)寫法
	/*BinaryTree<T>& operator=(const BinaryTree& t)
	{
		if (this != &t)
		{
			_DestroyTree(_root);
			_root = _CopyTree(t._root);
		}

		return *this;
	}*/

	//賦值運算符重載的現(xiàn)代寫法
	BinaryTree<T>& operator=(BinaryTree<T> t)
	{
		swap(_root, t._root);

		return *this;
	}

	//遞歸前序遍歷
	void PreOrderTraverse()
	{
		_PreOrderTraverse(_root);

		cout<<endl;
	}

	//遞歸中序遍歷
	void InOrderTraverse()
	{
		_InOrderTraverse(_root);

		cout<<endl;
	}

	//遞歸后序遍歷
	void PostOrderTraverse()
	{
		_PostOrderTraverse(_root);

		cout<<endl;
	}

	//非遞歸層序遍歷
	void LevelOrderTraverse()
	{
		if (NULL == _root)
		{
			return;
		}

		queue<BinaryTreeNode<T>*> q;
		q.push(_root);
		while (!q.empty())
		{
			BinaryTreeNode<T>* front = q.front();
			q.pop();
			cout<<front._data<<" ";

			if (front->_left)
			{
				q.push(front->_left);
			}

			if (front->_right)
			{
				q.push(front->_right);
			}
		}
	}
	
	//非遞歸前序遍歷
	void PreOrderTraverse_NonR()
	{
		if (NULL == _root)
		{
			return;
		}

		stack<BinaryTreeNode<T>*> s;
		s.push(_root);

		while (!s.empty())//當棧為空時遍歷完成
		{
			//先訪問根節(jié)點
			BinaryTreeNode<T>* top = s.top();
			s.pop();
			cout<<top->_data<<" ";

			//右節(jié)點存在時先入棧，后出棧
			if (top->_right)
			{
				s.push(top->_right);
			}

			//左結(jié)點存在時后入棧，先出棧
			if (top->_left)
			{
				s.push(top->_left);
			}
		}

		cout<<endl;
	}

	//非遞歸中序遍歷
	void InOrderTraverse_NonR()
	{
		if (NULL == _root)
		{
			return;
		}

		stack<BinaryTreeNode<T>*> s;
		BinaryTreeNode<T>* cur = _root;

		while (cur || !s.empty())
		{
			//左結(jié)點全部入棧
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}

			if (!s.empty())
			{
				BinaryTreeNode<T>* top = s.top();
				cout<<top->_data<<" ";
				s.pop();

				cur = top->_right;//將棧頂結(jié)點的右節(jié)點看作子樹的根節(jié)點
			}
		}

		cout<<endl;
	}

	//非遞歸后序遍歷
	void PostOrderTraverse_NonR()
	{
		if (NULL == _root)
		{
			return;
		}

		stack<BinaryTreeNode<T>*> s;
		BinaryTreeNode<T>* cur = _root;
		BinaryTreeNode<T>* pre = NULL;

		while (cur || !s.empty())//當前結(jié)點為空和棧為空同時滿足時遍歷完成
		{
			//左結(jié)點全部入棧
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}

			BinaryTreeNode<T>* top = s.top();

			if (NULL == top->_right || pre == top->_right)//若當前結(jié)點的右結(jié)點為空或者右節(jié)點已經(jīng)訪問過，可以訪問該結(jié)點
			{
				cout<<top->_data<<" ";
				pre = top;
				s.pop();
			}
			else//該結(jié)點的右節(jié)點不為空且未被訪問
			{
				cur = top->_right;//將該結(jié)點的右節(jié)點看作子樹的根節(jié)點
			}
		}

		cout<<endl;
	}

	//求結(jié)點數(shù)
	size_t Size()
	{
		size_t size = 0;
		_Size(_root, size);
		return size;
	}

	//求深度
	size_t Depth()
	{
		return _Depth(_root);
	}

	//求葉子結(jié)點數(shù)
	size_t LeafSize()
	{
		size_t leafSize = 0;
		_LeafSize(_root, leafSize);
		return leafSize;
	}

	//求第K層結(jié)點數(shù)
	size_t GetKLevel(const size_t& k)
	{
		 return _GetKLevel(_root, k);
	}
protected:
	BinaryTreeNode<T>* _CreateTree(const T* a, size_t size, size_t& index, const T& invalid)
	{
		BinaryTreeNode<T>* root = NULL;

		if (index < size && a[index] != invalid)
		{
			root = new BinaryTreeNode<T>(a[index]);
			root->_left = _CreateTree(a, size, ++index, invalid);
			root->_right = _CreateTree(a, size, ++index, invalid);
		}

		return root;
	}
	
	void _DestroyTree(BinaryTreeNode<T>* root)
	{
		if (NULL == root)
		{
			return;
		}

		if (NULL == root->_left && NULL == root->_right)
		{
			delete root;
			root = NULL;
			return;
		}

		_DestroyTree(root->_left);
		_DestroyTree(root->_right);
		delete root;
	}

	BinaryTreeNode<T>* _CopyTree(BinaryTreeNode<T>* root)
	{
		if (NULL == root)
		{
			return NULL;
		}

		BinaryTreeNode<T>* newRoot = new BinaryTreeNode<T>(root->_data);
		newRoot->_left = _CopyTree(root->_left);
		newRoot->_right = _CopyTree(root->_right);

		return newRoot;
	}

	void _PreOrderTraverse(BinaryTreeNode<T>* root)
	{
		if (NULL == root)
		{
			return;
		}

		cout<<root->_data<<" ";
		_PreOrderTraverse(root->_left);
		_PreOrderTraverse(root->_right);
	}

	void _InOrderTraverse(BinaryTreeNode<T>* root)
	{
		if (NULL == root)
		{
			return;
		}

		_InOrderTraverse(root->_left);
		cout<<root->_data<<" ";
		_InOrderTraverse(root->_right);
	}

	void _PostOrderTraverse(BinaryTreeNode<T>* root)
	{
		if (NULL == root)
		{
			return;
		}

		_PostOrderTraverse(root->_left);
		_PostOrderTraverse(root->_right);
		cout<<root->_data<<" ";
	}

	//_Size方法1：
	/*size_t _Size(BinaryTreeNode<T>* root)
	{
		if (NULL == root)
		{
			return;
		}

		return _Size(root->left) + _Size(root->_right) + 1;
	}*/

	//_Size方法2：（存在線程安全問題）
	/*size_t _Size(BinaryTreeNode<T>* root)
	{
		static size_t size = 0;
		if (NULL == root)
		{
			return 0;
		}
		else
		{
			++size;
		}

		_Size(root->_left);
		_Size(root->_right);

		return size;
	}*/

	//_Size方法3：
	void _Size(BinaryTreeNode<T>* root, size_t& size)
	{
		if (NULL == root)
		{
			return;
		}
		else
		{
			++size;
		}

		_Size(root->_left, size);
		_Size(root->_right, size);
	}

	size_t _Depth(BinaryTreeNode<T>* root)
	{
		if (NULL == root)
		{
			return 0;
		}

		size_t leftDepth = _Depth(root->_left);
		size_t rightDepth = _Depth(root->_right);

		return leftDepth > rightDepth ? leftDepth+1 : rightDepth+1;
	}

	void _LeafSize(BinaryTreeNode<T>* root, size_t& leafSize)
	{
		if (NULL == root)
		{
			return;
		}

		if (NULL == root->_left && NULL == root->_right)
		{
			++leafSize;
			return;
		}

		_LeafSize(root->_left, leafSize);
		_LeafSize(root->_right, leafSize);
	}

	size_t _GetKLevel(BinaryTreeNode<T>* root, const size_t& k)
	{
		assert(k > 0);

		if (NULL == root)
		{
			return 0;
		}

		if (k == 1)
		{
			return 1;
		}

		return _GetKLevel(root->_left, k-1) + _GetKLevel(root->_right, k-1);
	}
protected:
	BinaryTreeNode<T>* _root;
};

void BinaryTreeTest()
{
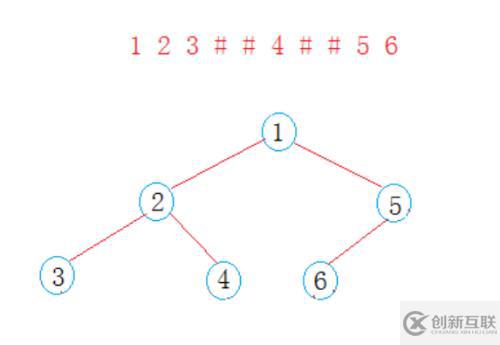
	int a[] = {1, 2, 3, '#', '#', 4, '#', '#', 5, 6};
	BinaryTree<int> t(a, sizeof(a)/sizeof(a[0]), '#');

	cout<<"遞歸前序遍歷：";
	t.PreOrderTraverse();
	cout<<"遞歸中序遍歷：";
	t.InOrderTraverse();
	cout<<"遞歸后序遍歷：";
	t.PostOrderTraverse();
	cout<<"非遞歸前序遍歷：";
	t.PreOrderTraverse_NonR();
	cout<<"非遞歸中序遍歷：";
	t.InOrderTraverse_NonR();
	cout<<"非遞歸后序遍歷：";
	t.PostOrderTraverse_NonR();

	cout<<"Size:"<<t.Size()<<endl;
	cout<<"Depth:"<<t.Depth()<<endl;
	cout<<"LeafSize:"<<t.LeafSize()<<endl;
	cout<<"Get3Level:"<<t.GetKLevel(3)<<endl;

	BinaryTree<int> t2(t);
	cout<<"t2:";
	t2.PreOrderTraverse();

	BinaryTree<int> t3;
	t3 = t2;
	cout<<"t3:";
	t3.PreOrderTraverse();
}

int main()
{
	BinaryTreeTest();

	return 0;
}

生成的二叉樹如下圖：

為天壇街道等地區(qū)用戶提供了全套網(wǎng)頁設(shè)計制作服務(wù)，及天壇街道網(wǎng)站建設(shè)行業(yè)解決方案。主營業(yè)務(wù)為成都網(wǎng)站建設(shè)、做網(wǎng)站、天壇街道網(wǎng)站設(shè)計，以傳統(tǒng)方式定制建設(shè)網(wǎng)站，并提供域名空間備案等一條龍服務(wù)，秉承以專業(yè)、用心的態(tài)度為用戶提供真誠的服務(wù)。我們深信只要達到每一位用戶的要求，就會得到認可，從而選擇與我們長期合作。這樣，我們也可以走得更遠！

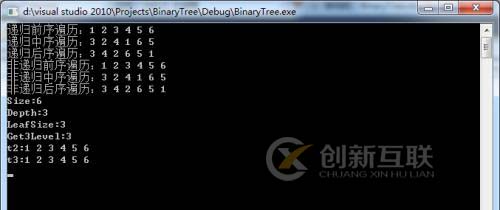
測試結(jié)果：

分享標題：C++實現(xiàn)二叉樹
網(wǎng)頁地址：http://chinadenli.net/article30/ihojpo.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供云服務(wù)器、網(wǎng)站策劃、網(wǎng)站改版、網(wǎng)站維護、外貿(mào)建站、網(wǎng)站建設(shè)

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)