什么是對稱矩陣（SymmetricMatrix）？

創(chuàng)新互聯(lián)IDC提供業(yè)務(wù):成都服務(wù)器托管,成都服務(wù)器租用,成都服務(wù)器托管,重慶服務(wù)器租用等四川省內(nèi)主機托管與主機租用業(yè)務(wù);數(shù)據(jù)中心含:雙線機房,BGP機房,電信機房,移動機房,聯(lián)通機房。

對稱對稱-------看

設(shè)一個N*N的方陣A，A中任意元素Aij，當(dāng)且僅當(dāng)Aij == Aji(0 <= i <= N-1 && 0 <= j <= N-1)，則矩陣A是對稱矩陣。以矩陣的對角線為分隔，分為上三角和下三角。

壓縮存就是矩陣存儲時只需要存儲上三角/下三角的數(shù)據(jù)，所以最多存儲n(n+1)/2個數(shù)據(jù)。

對稱矩陣和壓縮存儲的對應(yīng)關(guān)系：下三角存儲i>=j,  SymmetricMatrix[i][j] == Array[i*(i+1)/2+j]

那么，我們該如何存儲呢？

按照一元數(shù)組的方法，存儲下三角的元素即可。

template<class T>
class SymmetricMatrix
{
public:
	SymmetricMatrix(T* a, size_t size, size_t n)
		:_data(new T[n*(n + 1) / 2])    //開辟好數(shù)組一半大小的空間
		, _size(size)
		, _n(n)
	{
		size_t index = 0;
		for (size_t i = 0; i < _n; i++)
		{
			for (size_t j = 0; j < _n; j++)
			{
				if (i >= j)                    //下三角元素
				{
					_data[index++] = a[i*n + j];
				}
				else
				{
					break;
				}
			}
		}
	}
public:
	void Display()
	{
		size_t index = 0;
		for (size_t i = 0; i < _n; i++)
		{
			for (size_t j = 0; j < _n; j++)
			{
				if (i >= j)
				{
					cout << _data[i*(i + 1) / 2 + j]<<" ";
				}
				else   //上三角位置
				{
					cout << _data[j*(j + 1) / 2 + i]<<" ";  //交換行列坐標(biāo)
				}
			}
			cout << endl;
		}
		cout << endl;
	}
	//獲取某行某列元素
	T& Access(size_t i, size_t j)
	{
		if (i < j)
		{
			swap(i, j);
		}
		return _data[i*(i + 1) / 2 + j];
	}
protected:
	T* _data;
	size_t _size;
	size_t _n;
};

什么又是稀疏矩陣呢？

壓縮存儲值存儲極少數(shù)的有效數(shù)據(jù)。使用{row,col,value}三元組存儲每一個有效數(shù)據(jù)，三元組按原矩陣中的位置，以行優(yōu)先級先后順序依次存放。

首先構(gòu)建三元組（這里的每一個三元組就是矩陣中的一個元素）

template<class T>
struct Triple
{
	T _value;
	size_t _col;
	size_t _row;
	Triple(const T& value = T(), size_t row = 0, size_t col = 0)
		:_value(value)
		, _row(row)
		,_col(col)
	{}
};

再存儲有效值。

創(chuàng)建一個類，在構(gòu)造函數(shù)中我們實現(xiàn)有效值的存儲

SparseMatrix(T* a, size_t m, size_t n, const T& invalid)
		:_rowSize(m)
		, _colSize(n)
		, _invalid(invalid)
	{
		for (size_t i = 0; i < _rowSize; i++)
		{
			for (size_t j = 0; j < _colSize; j++)
			{
				if (a[i*n + j] != _invalid)
				{
					_a.push_back(Triple<T>(a[i*n + j], i, j));
				}
			}
		}
	}
	SparseMatrix()
		:_rowSize(0)
		, _colSize(0)
		, _invalid(0)
	{}

這里還有一個矩陣轉(zhuǎn)置。何為矩陣轉(zhuǎn)置呢？

*矩陣轉(zhuǎn)置

將原矩陣的行、列對換，也就是將[i][j]和[j][i]位置上的數(shù)據(jù)對換。

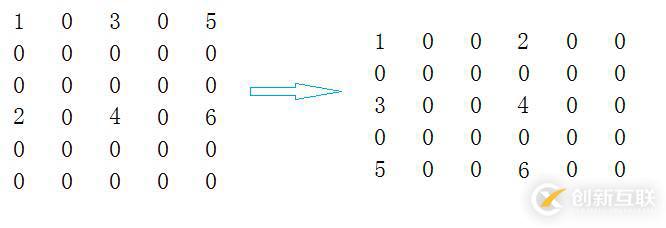
SparseMatrix<T> Transport()
	{
		SparseMatrix<T> tmp;
		tmp._colSize = _rowSize;  //交換行列大小
		tmp._rowSize = _colSize;
		tmp._invalid = _invalid;
		
		
		for (size_t i = 0; i < _colSize; i++)    
		{
			size_t index = 0;
			while (index < _a.size())
			{
				if (_a[index]._col == i)    //按照列在存儲的三元組中依次尋找.
				{                           //找到列為0，壓入新的順序表中，繼續(xù)找.....
					Triple<T> t;
					t._col = _a[index]._row;
					t._row = _a[index]._col;
					t._value = _a[index]._value;
					tmp._a.push_back(t);
				}
				index++;
			}

		}
		return tmp;
	}

你們有沒有發(fā)現(xiàn)普通轉(zhuǎn)置的效率太低，時間復(fù)雜度太高？它的時間復(fù)雜度為O（列數(shù)*有效數(shù)據(jù)的行數(shù)),那我接下來就給大家介紹快速轉(zhuǎn)置。

快速轉(zhuǎn)置，只需要遍歷一次存儲的有效數(shù)據(jù)。這個怎么做到呢？

我們需要得出轉(zhuǎn)置后每一行有效值的個數(shù)和每一行第一個有效值在壓縮矩陣中的起始位置。

即

RowCounts = { 2 , 0 , 2 , 0 , 2 } ;

RowStart = { 0 , 2 , 2 , 4 , 4 } ;

我們可以看出 RowStrat[0] 總是恒為 0，那很容易就可以發(fā)現(xiàn)

 RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];

再看代碼

SparseMatrix<T> FastTransport()
	{
		SparseMatrix<T> tmp;
		tmp._colSize = _rowSize;
		tmp._rowSize = _colSize;
		tmp._invalid = _invalid;
		tmp._a.resize(_a.size());

		int *RowCounts = new int[_colSize];
		int *RowStart = new int[_colSize];
		memset(RowCounts, 0, sizeof(int)*_colSize);
		memset(RowStart, 0, sizeof(int)*_colSize);

		//統(tǒng)計個數(shù)
		size_t index = 0;
		while (index < _a.size())
		{
			RowCounts[_a[index]._col]++;
			index++;
		}
		RowStart[0] = 0;
		for (size_t i = 1; i < _colSize; i++)
		{
			RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];
		}

		//定位位置
		index = 0;
		while (index < _a.size())
		{
			int rowindex = _a[index]._col;
			int& start = RowStart[rowindex];
			Triple<T> t;
			t._col = _a[index]._row;
			t._row = _a[index]._col;
			t._value = _a[index]._value;
			tmp._a[start] = t;
			start++;
			index++;
		}
		delete[] RowCounts;
		delete[] RowStart;

		return tmp;
	}

接下來我們繼續(xù)使用行優(yōu)先的原則將壓縮矩陣打印出來

void Display()
	{
		size_t index = 0;
		for (size_t i = 0; i < _rowSize; i++)
		{
			for (size_t j = 0; j < _colSize; j++)
			{
				if (index < _a.size()&&_a[index]._row == i&&_a[index]._col == j)
				{
					cout << _a[index]._value << " ";
					index++;
				}
				else
				{
					cout << _invalid << " ";
				}
			}
			cout << endl;
		}
		cout << endl;
	}

最后再補上我們類的成員變量

protected:
	vector<Triple<T>> _a;
	size_t _rowSize;
	size_t _colSize;
	T _invalid;

這就是我們的快速轉(zhuǎn)置了。小伙伴們好好看哦。我會繼續(xù)努力噠~

另外有需要云服務(wù)器可以了解下創(chuàng)新互聯(lián)scvps.cn，海內(nèi)外云服務(wù)器15元起步，三天無理由+7*72小時售后在線，公司持有idc許可證，提供“云服務(wù)器、裸金屬服務(wù)器、高防服務(wù)器、香港服務(wù)器、美國服務(wù)器、虛擬主機、免備案服務(wù)器”等云主機租用服務(wù)以及企業(yè)上云的綜合解決方案，具有“安全穩(wěn)定、簡單易用、服務(wù)可用性高、性價比高”等特點與優(yōu)勢，專為企業(yè)上云打造定制，能夠滿足用戶豐富、多元化的應(yīng)用場景需求。

分享題目：矩陣-----對稱矩陣及其壓縮存儲&&稀疏矩陣-創(chuàng)新互聯(lián)
URL鏈接：http://chinadenli.net/article2/dpidic.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供網(wǎng)站排名、域名注冊、品牌網(wǎng)站建設(shè)、品牌網(wǎng)站制作、外貿(mào)網(wǎng)站建設(shè)、網(wǎng)站改版

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)